Introduction In order to extend the battery lifetime of portable type electric instruments, saving the electric power consumption of the devices is a quite important subject, even for the liquid crystal display (LCD). LCD is used for various uses, especially for the mobile application, because of its light weight and low electric power consumption. Now, bistable type LCDs such as a zenithal bistable display (ZBD) attracted great attention [1]. A ZBD device based on surface relief grating alignment has demonstrated good image quality and memory capability. However, the exact mechanism of the alignment remains a debatable topic. Hallam and Sambles arranged the argument with regard to a topological alignment model [2]. In their article, surface azimuthal anchoring energy as a function of the grating height was calculated by Berreman's topological alignment model on a basis of the liquid crystal (LC) elastic theory [3]. From the comparison with the calculation and experimental results by means of the optical guided mode technique, a good agreement was found for shallow amplitude gratings, but not for larger amplitude gratings. They enumerated possible causes of this discrepancy, and described the demand of more comprehensive topological model. A possible cause of the contradiction could be due to their low experimental accuracy. Another verification experiment is required. The finite element method (FEM) is widely used for solving the two- and/or three-dimensional problems. The liquid crystal alignment can be also analyzed by FEM simulation. Recently, a saturation tendency of surface azimuthal anchoring energy as a function of the height of the grating was well demonstrated by a numerical simulation on a basis of FEM [4]. Furthermore, a good agreement with FEM calculation and experimental results was also shown not only for shallow amplitude gratings surface, but also for deep groove gratings. In this paper, dependence of the shape of the grating surface on the surface azimuthal anchoring energy is studied by FEM, in consideration of practical grating surfaces. Finite Element Method To analyze two-dimensional director arrangement on a sinusoidal relief grating surface, two-dimensional Finite Element Method (FEM) was used basing on an elastic theory with energy minimization principle. Figure 1 represents a typical result from a two-dimensional FEM simulation, where mesh 30 x 10 nodes were arranged. Rods in Figure 1 represent LC director, and the center of the LC molecule corresponds to the node. A periodic boundary condition was applied to the left side and right side lateral boundary. With regard to the upper boundary condition, LC directors were set to parallel alignment along the glass substrate, which corresponds to the director arrangement in the bulk. 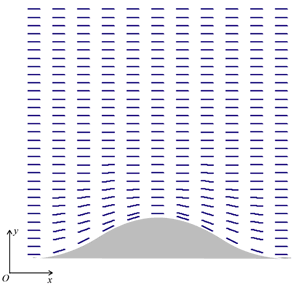
Figure 1. Typical result from a two dimensional FEM simulation. Rod represents the LC director. With regard to the lower boundary surface, a sinusoidal relief grating was assumed with a pitch of the sinusoidal relief grating, P corresponds to the one period of the mesh. At all nodes on the lower surface, as shown in Figure 1, parallel alignment of LC molecules as a fixed boundary condition was assumed. Because, molecules align perpendicular to the ridgelines, the elastic distortion energy is the maximum. In a considered area e, when θ(x, y) as a function of the location (x, y) is defined by the angle between the director and x axis, the Frank's elastic energy density can be derived [5],  (1) (1)
where K11 and K33 are the elastic constants for splay and bend deformation [5]. The matrix of FEM can be formularized by the linear approximation of θ(x, y). As is described in the past literature [3], if the molecules lie parallel to the ridges, there is no distortion energy near the surface. felas represents extra elastic energy par unit area that can be released by reorientating molecules parallel along the ridges. i. e., the elastic distortion energy in the considered area e corresponds to the surface azimuthal anchoring energy function F8. When F8 is expressed by  (2) (2)
where ΔΦ is the deviation angle between the director and ridgeline, the surface azimuthal anchoring energy coefficient Aφ can be obtained by  (3) (3)
since ΔΦ = 90˚ under the condition in our study [2,3]. Because, as is shown in equation (2), estimated Fs is maximum when ΔΦ = 90˚. To compare with the results of Berreman's model, the azimuthal anchoring energy was also calculated by the following equation [3];  (4) (4)
where h is the height of the gratings, Λ is the pitch of the gratings and K=(K11 + K33)/2. The elastic constants of LC materials K11 and K33 were preliminary measured by the Koyama’s method and listed in Table 1. Table 1. The elastic constants of LC materials | | | MLC-2051 | 10.4 × 10-12 N | 15.6 × 10-12 N | | 5CB | 7.12 × 10-12 N | 9.82 × 10-12 N | The shape of the actual relief grating formed experimentally would be asymmetrical rather than sinusoidal. To investigate the dependence of the shape of the grating surface on the surface azimuthal anchoring energy, asymmetric sinusoidal grating and trapezoid shaped grating surface are supposed, as shown in Figures 2 and 3, where the parameters W and D represent a ratio of asymmetry against P. 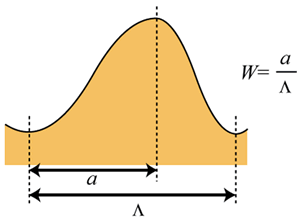
Figure 2. The shape of the asymmetric sinusoidal grating calculated in this study. 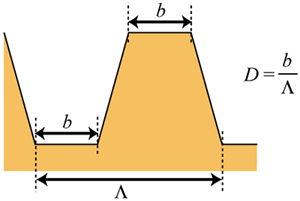
Figure 3. The shape of the trapezoid grating calculated in this study. Experimental Gratings used in our experiment were fabricated by photoresist (Shipley S1830). After coating a photoresist film on a borosilicate glass substrate, holographic UV light was irradiated on the photoresist film. Figure 4 shows the experimental setup for the holographic light. 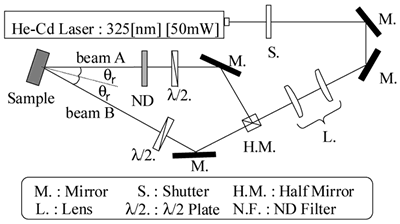
Figure 4. Experimental setup of the holographic UV light Gratings were written by using two linearly polarized, mutually coherent cw He-Cd laser beams (Kimmon K3501R-G), whose wavelength λ = 325 nm. Λ is determined by the crossing angle θr between the two laser beams, which is described by  (5) (5)
We carried out these experiments when Λ = 2, 3, 4 μm respectively. Height of the gratings was controlled by the intensity of UV laser beams. After finishing UV exposure, the average height of the gratings was measured by atomic force microscope (Shimadzu SPM-9500 J2). Twisted nematic LCD sample cells were fabricated by combining a grating substrate and another glass substrate on which polyvinyl alcohol (PVA) was coated and pre-rubbed. Nominal cell gap was 25 μm. Chemical feature may play an important role to the anchoring energy. Especially, the effect of surface wettability and surface adsorption on the anchoring energy have been debated for a decade. Therefore, two kinds of nematic LCs, a mixture (MLC-2051, Merck Japan) and 4-cyano-4'-n-pentylbiphenyl (5CB, Merck Japan), were employed. The former is bulk transition type (relatively low wettability) LC, the latter is surface transition type (high nematic wettability) LC [7]. Azimuthal anchoring energy was measured by a torque balance method [8]. The deviation angle ΔΦ from the ridgeline of the gratings indicates the azimuthal anchoring energy Aφ caused by the relief grating. Here, we assume that the azimuthal anchoring at the PVA surface is relatively strong against the grating surface. [9] Aφ is determined by the balance between the torque due to the bulk and that due to surface anchoring. The azimuthal anchoring energy Aφ can be given from the elastic theory of the nematic liquid crystals as [8]  (6) (6)
 (7) (7)
where d is the cell thickness, Φt is the actual twist and Φt0 is the angle between the directions of rubbing treatment for the PVA alignment films and the ridgeline of the gratings. In our experiments, unlike the previous paper [8], tungsten lamp as a white light source was used in order to avoid the erroneous influence of strong absorption by the photoresist. Since the measured cell is so thick that it fulfills Mauguin’s conditions [10], Φt corresponds to the angle between the found extinction position by rotating the polarizer and analyzer. Results and Discussion Figure 5 shows the numerical results of the surface azimuthal anchoring energy as a function of the grating height calculated by the Berreman's model and by the FEM. The pitch of the gratings were supposed to be 2, 3 and 4 μm. The LC material was MLC-2051. From Figure 5, a saturation tendency of surface azimuthal anchoring energy as a function of the grating height was found in both calculation methods. Though the saturation tendency calculated by FEM is more remarkable than that calculated by Berreman's model, it seems that two calculations are mutually in agreement. The experimental results are also plotted on Figure 5. From our experimental results, the height of 0.2 ~ 1.5 μm gratings shows good agreement in both calculations. 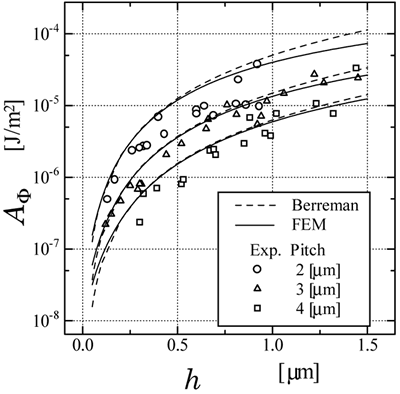
Figure 5. Experimental and numerical results of surface azimuthal anchoring energy as a function of grating height calculated by Berreman's model and FEM, where the LC material is MLC-2051. To verify our consideration, another study using 5CB was carried out. To emphasize the distinct saturation tendency which differs from the Berremen's original linear dependency, the results of the square of the grating height versus Aφ as in ref. [2] are shown in Figure 6. Regardless of the LC materials, the saturation tendency for the large-amplitude grating surface and a good agreement between the numerical and experimental results for the shallow grating surface were clearly recognized. This result indicates that the elastic energy is dominant rather than the chemical nature, except unexpected surface conditions such as the strong homeotropic alignment at the grating surface. 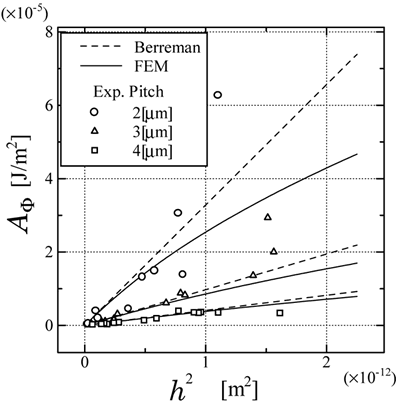
Figure 6. Experimental and numerical results of surface azimuthal anchoring energy as a function of square of grating height calculated by Berreman's model and FEM, where the LC material is 5CB. Asymmetric sinusoidal grating can be easily obtained by the holographic relief gratings in which the irradiation angle is set to be asymmetric. Figure 7 shows the numerical results of the surface azimuthal anchoring energy caused by the asymmetric sinusoidal grating as a function of the grating height calculated by the FEM, for LC material as MLC-2051. It is found that asymmetric sinusoidal grating shows strong azimuthal anchoring energy. 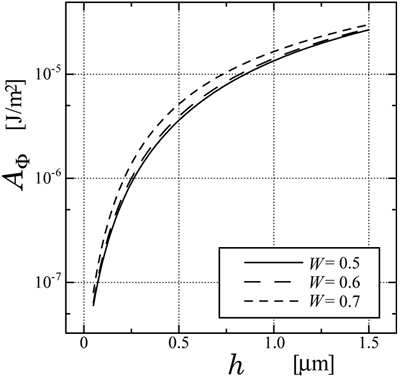
Figure 7. Numerical results of surface azimuthal anchoring energy caused by the asymmetric sinusoidal grating as a function of grating height calculated by FEM. As is often seen by using electron microscope, the shape of the photoresist is trapezoid rather than rectangle. Therefore, the shape of the relief grating made by the photomask process seems to be trapezoid. Figure 8 shows the numerical results of the surface azimuthal anchoring energy caused by the trapezoid grating as a function of the grating height calculated by the FEM. When the shape of the gratings is triangle (D=0), the azimuthal anchoring energy is relatively small and depends on the height of the gratings. On the other hand, when the shape of the gratings is rectangular (D=0.5), the azimuthal anchoring energy is strong and less sensitive to the height of the gratings. This is because we assumed that the director just above the surface tends to lie parallel along the surface, as a result, the director near the lateral surface of the rectangle aligns normal to the substrate. The director profile calculated by the FEM is shown in Figure 9, where D=0.4. It is found that the director profile calculated by FEM is impartial and appropriate. 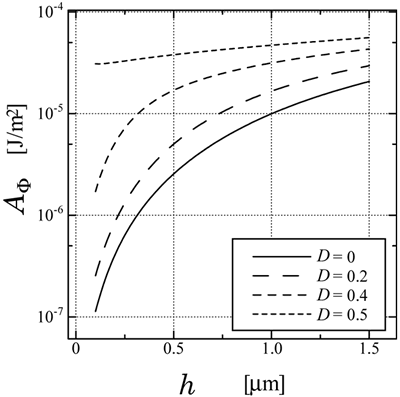
Figure 8. Numerical results of surface azimuthal anchoring energy caused by the trapezoid grating as a function of grating height calculated by FEM. 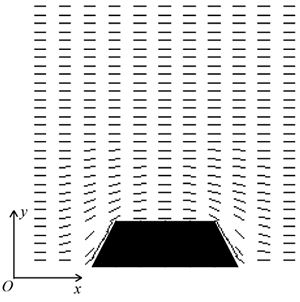
Figure 9. Director profile calculated by the FEM (D=0.4). Conclusions It is verified by FEM that Berreman's topological alignment model is applicable for shallow grating surface. The disagreement between the theoretical analysis and experimental results reported by ref. [2] seems to be caused by the limit of Berreman's model rather than the experimental failure. Simple approximation for surface anchoring formula as the similar level as the Berreman's evaluation can explain such saturation tendency, and the anchoring effect is dominated by the elasticity rather than the chemical nature. To design the surface azimuthal anchoring energy of the arbitrary surface shape of the relief gratings, FEM can be a powerful tool. Because, after tracing the real surface by using atomic force microscope, traced pattern can be directly input to FEM, and the surface azimuthal anchoring energy can be predicted by FEM. Acknowledgements We appreciate Mr. H. Ichinose (Merck Japan) for providing LC materials. This work is supported by Grant-in-Aid (No.15760020) for Young Scientists (B) of Japan Society for the Promotion of Science. References 1. G. P. Bryan-Brown, C. V. Brown, J. C. Jones, E. L. Wood, I. C. Sage, P. Brett and J. Rudin, “Grating Aligned Bistable Nematic Device”, Society for Information Display'97 Digest, (1997) p.37-40. 2. B. T. Hallam and J. R. Sambles, “Groove depth dependence of the anchoring strength of a zero order grating-aligned liquid crystal”, Liquid Crystals, 27 (2000) 1207-1211. 3. D.W. Berreman, “Solid Surface Shape and the Alignment of an Adjacent Nematic Liquid Crystal”, Phys. Rev. Lett., 28 (1972) 1683-1686. 4. Y. Ohta, N. Tanaka, M. Kimura and T. Akahane, “Surface Azimuthal Anchoring Energy between the Grating Surface and Nematic Liquid Crystal Layer Studied by Finite Element Method”, Jpn. J. Appl. Phys., 43 (2004) 4310-4311. 5. F. C. Frank, “Liquid crystals: On the theory of liquid crystals”, Disc. Faraday Soc., 25 (1958) 19-28. 6. K. Koyama, M. Kawaida and and T. Akahane, “A Method for Determination of Elastic Constants K1, K2, K3 of a Nematic Liquid Crystal Only Using a Homogeneously Aligned Cell”, Jpn. J. Appl. Phys., 28 (1989) 1412-1416. 7. S. Oka, T. Mitsumoto, M. Kimura and T. Akahane, “Relationship between surface order and surface azimuthal anchoring strength of nematic liquid crystals” Phys. Rev. E, 69, 061711 (2004). 8. T. Akahane, H. Kaneko and M. Kimura, “Novel Method of Measuring Surface Torsional Anchoring Strength of Nematic Liquid Crystals”, Jpn. J. Appl. Phys., 35 (1996) 4434-4437. 9. K. Okubo, M. Kimura and T. Akahane, “Measurement of Genuine Azimuthal Anchoring Energy in Consideration of Liquid Crystal Molecular Adsorption on Alignment Film”, Jpn. J. Appl. Phys., 42 (2003) 6428-6433. 10. C. H. Gooch and H.A. Tarry, “The optical properties of twisted nematic liquid crystal structures with twist angles ≤ 90°” , J. Phys., D8 (1975) 1575-1584. Contact Details |