Characterization of Elastic-Plastic (Stress-Strain) Behavior of Materials in Small Volumes by Spherical Indentation

The nanoindentation technique is extensively used for characterization of mechanical properties in small volumes. Due to its local character, the nanoindentation technique has also recently been used for the determination of local stress-strain (elastic-plastic) properties.

Characterization of Elastic-Plastic (Stress-Strain) Behavior of Materials in Small Volumes by Spherical Indentation

For this, spherical indentation is used and representative stress and strain values according to Tabor are calculated. This application report resents the results of this method in several applications including spherical particles, welds, mechanical intermixing and polymers.

Introduction

Since the work of Tabor in 1951¹ there has been growing interest in determination of stress-strain curves from indentation methods^2–4. This was mainly due to the fact that indentation allowed testing of materials in small volumes – in contrary to conventional tensile testing that requires relatively large specimens. This interest in local stress-strain properties increased even more with the development and routine use of instrumented indentation (IIT). The IIT technique allows full control of the indentation parameters while recording force and displacement and thanks to its force and displacement resolutions it is suitable for testing very thin films or small volumes.

Although the IIT uses mostly sharp tipped indenters such as Berkovich, spherical indenters have the advantage of increasing the strain with increasing load. This fact is used in the indentation stress-strain methods for local characterization of elastic-plastic properties. Diamond or ruby indenters with radii of 10 μm up to 200 μm are typically used in these experiments. The choice of radius depends on the stiffness of the tested material, thickness of the film or size of structural units that should be characterized^5,6.

For determination of elastic-plastic behavior of metals (but also of other materials) the definitions of indentation stress and representative strain proposed by Tabor¹ are often used. Although these definitions are only approximate, they are widely accepted and have since been verified by other investigators^2,4,5. In these equations, the indentation (or representative) strain is given by:

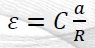(1)

where £ is the representative strain, a is the contact radius and R is radius of the indenter. C is a constant which is usually taken to be 0.2. The indentation representative stress σ is defined as (see Figure 1)

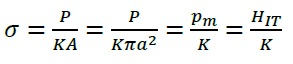(2)

where P is load, a is contact radius, P_m is mean pressure (=hardness) and K is the constraint factor (3 for most perfectly plastic engineering materials⁷).

Figure 1. Schematic illustration of spherical indentation⁷. h_m is the indentation depth.

Want to know more? Click here to read the full article.

This information has been sourced, reviewed and adapted from materials provided by Anton Paar GmbH.

For more information on this source, please visit Anton Paar GmbH.