How to Reveal Elastic Microstructures in a Monolithic Glass

The exceptional sensitivity of atomic force microscopy and nanoindentation allows for the evaluation of minute displacements as low as the sub-nanometer system, allowing mechanical attributes (such as mechanical moduli) to be tested without damaging the elastic response limit.

For the shallow indentation depths common in nanomechanical testing, the assumption by the Hertzian model of a flat surface for the tip-sample interaction is often inaccurate. This is because the model does not account for surface roughness, which can lead to errors in calculating modulus amplitudes if overlooked in the analysis.

This article discusses the challenge of non-flat surface conditions in monolithic metallic glass and how to adjust for curvature-induced effects on the indentation modulus using an equivalent radius.¹ This adjustment reveals an elastic microstructure within the metallic glass, which consists solely of a single amorphous phase.

The results showcase the capability of nanoindentation and atomic force microscopy to uncover material properties that are not detectable through other techniques.

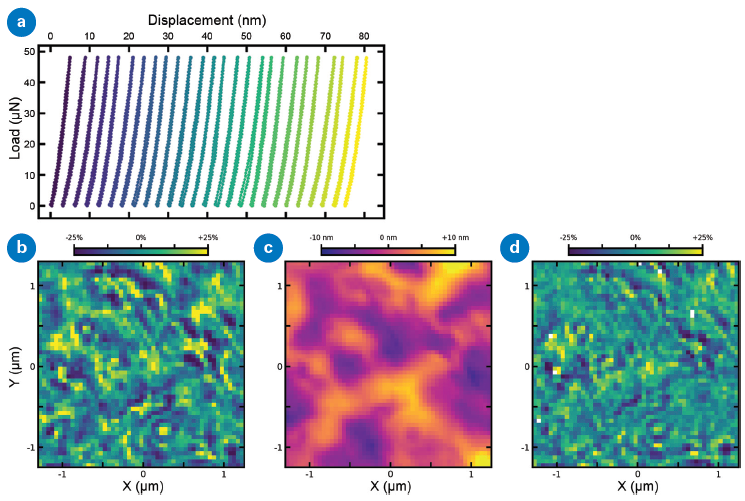
(a) Representative examples of load-displacement curves measured on a bulk metallic glass surface within the elastic response limit. (b) Mechanical modulus deduced from curves in (a) by the Oliver-Pharr method. (c) Topography measured for the same region on the sample surface as shown in (b). (d) Mechanical modulus for the corresponding area after correcting for topography-induced effects. Image Credit: Bruker Nano Surfaces and Metrology

Mechanical Mapping

Spatially resolved nanomechanical measurements were performed on a well-polished surface of the bulk metallic glass using a Hysitron TI 980 TriboIndenter^®, equipped with a cono-spherical tip with a diameter of 890 nm.

The surface was analyzed using accelerated property mapping (XPM^™) across a lateral area of 2.5 µm × 2.5 µm, examining both the mechanical modulus (shown in Figure 1b) and the topography (shown in Figure 1c).²

Representative local load-displacement curves, measured at an indentation depth of 50 nm, are presented in Figure 1a.

Topography Correction

Although variations in height across the width of a single indent are typically within the range of a few nanometers, the depth of indentation is similarly small. This creates a clear correlation between the material's modulus and its surface topography.^1,3 To account for the effects of curvature on the elastic modulus, an equivalent radius is calculated for each point within the mapped area.⁴

Therefore, the local curvature of the measured surface is defined as the inverse of the pair of independent local surface radii, namely, the radii of curvature,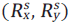. When considered with the tip radius, R_tip, these are the basis for calculating the equivalent radius,  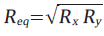by 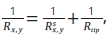 resulting in Equation 1.

Equation 1:

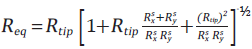The independent equivalent radii, denoted as (R_x,R_y), are illustrated in Figure 2. These radii are smaller than the tip radius when the local surface curvature is positive (such as at a peak on the surface), equal to the tip radius when the curvature is zero (indicating a flat surface with a constant slope), and larger than the tip radius when the curvature is negative.

In special cases where the equivalent radii approach infinity, the curvatures are near −1/R_tip​. In these scenarios, surface depressions with curvatures lower than this limit result in multiple contact points between the tip and the sample surface. This leads to measured curvatures equal to −1/R_tip, which do not accurately represent the actual, more extreme curvatures (<−1/R_tip) of the surface.

Results

To calculate the equivalent radius from measured topography data, the independent radii of curvature, 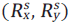, is related to the Gaussian and mean curvature, K^s and H^s.^1,4

Equation 2:

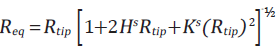These are determined by the first and second derivatives of the surface topography and can be evaluated through a point-by-point analysis of the data.

Equation 3:

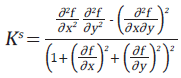Equation 4:

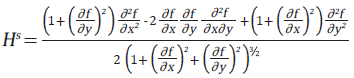Using the equivalent radius, the corrected elastic modulus, _Ec​, is calculated from the measured modulus, E_r​, and the tip radius, based on Hertzian contact mechanics via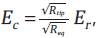 as depicted in Figure 1d.

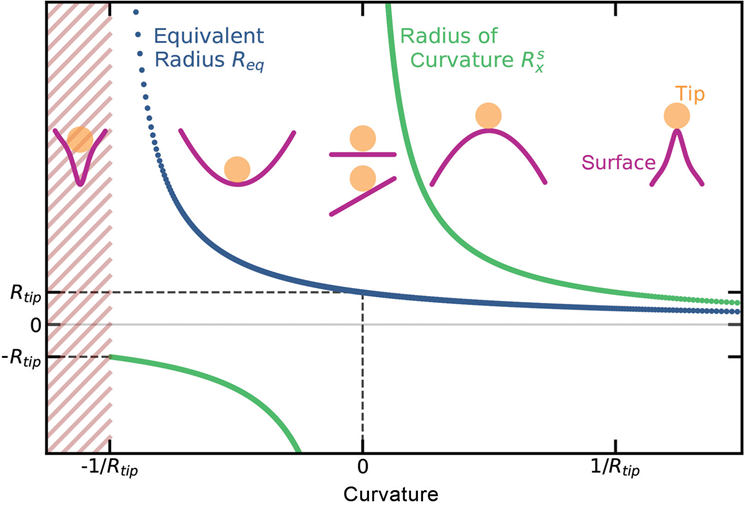
Equivalent radius and radius of curvature as a function of curvature with schematic representations of the interplay between surface curvature and tip. Image Credit: Bruker Nano Surfaces and Metrology

Conclusions

High-throughput, spatially resolved nanoindentation techniques can detect nanoelastic fluctuations in single-phase solids, as shown in this study of monolithic glass. These high-resolution measurements are particularly sensitive to long-wavelength topographical modulations with amplitudes of just a few nanometers.

A method outlined in References 1 and 4 significantly reduces the impact of topography-related effects on the elastic modulus.

Using the same tip for both topography and modulus measurements prevents scenarios that would lead to imaginary solutions for the equivalent radius. At locations where the radii of curvature approach the negative value of the tip radius, diverging values of the equivalent radius are anticipated.

Acknowledgments

Data courtesy of B. Riechers, R. Rashidi, and R. Maass, BAM, Berlin, Germany

Produced from materials originally authored by Dr. Birte Riechers, Federal Institute of Materials Research and Testing (BAM), Germany Prof. Dr. Robert Maass, Federal Institute of Materials Research and Testing (BAM), Germany Dr. Douglas Stauffer, Bruker.

References and Further Reading

1. Riechers et al., Materials & Design 229, 111929 (2023).
2. Hintsala et al., JOM 70, 494-503 (2018).
3. Tsai et al., Acta Materialia 139, 11-20 (2017).
4. Campbell et al., International Journal of Mechanical Sciences 161, 105015 (2019)

This information has been sourced, reviewed and adapted from materials provided by Bruker Nano Surfaces and Metrology.

For more information on this source, please visit Bruker Nano Surfaces and Metrology.