Introduction Nanostructured TiO2 is extensively studied as a very promising material for applications in sensors [1], photocatalysis [2], solar energy conversion [3] and optical coatings [4]. The properties of titania are determined by its different polymorphs. Thermodynamically stable rutile phase is obtained by thermal annealing from anatase, and its bulk phase transition occurs above 800°C [5]. However, the transformation in nanostructured titania is influenced by the method of synthesis, for example TiO2 prepared by hydrolysis can be obtained at 600°C [6], while films produced by sol-gel dip coating the anatase is the predominant phase even after heating at 800°C [7]. When titania is synthesized by the sol-gel processing, hydrolysis or colloidal chemistry methods, the as-prepared material presents an amorphous structure, therefore a thermal annealing is necessary to obtain a well-defined nanocrystalline phase and to eliminate contamination arising from the synthesis method [8]. The phase transition is accompanied by microstructural changes, such as densification, grain growth and porosity modification [9]. This indicates that the microstructure and the crystalline phase of the as-prepared sample influence the kinetics of the above mentioned processes. The annealing process significantly changes, at the same time, the microstructure, the crystalline phase and the nanoparticle dimensions of nanostructured titania[10]. The sol-gel synthesis favors the formation of vacancies and defects in the titania structure that may modify its catalytic properties [11]. Dehydration processes in sol-gel titania emulsions may affect its overall catalytic performance. Since 1978 [12] the photoacoustic techniques have experienced great expansion. Nowadays they are used in a wide range of scientific disciplines to carry out studies of diverse properties of condensed matter including optical, transport, and thermal properties [13-15]. The photoacoustic technique has been used in the characterization of a wide variety of materials, measuring, their thermal diffusivity [16-18] and thermal effusivity [19, 20]. Thermal effusivity has been previously used in the study of the time evolution of dynamical systems in which polymerization and dehydration is involved [12,21]. In this case a modified version of the conventional Rosencwaig cell has been used. In this work the evolution of the thermal effusivity as a function of time is monitored during the process of dehydration in aqueous thermally treated titania sample, obtained by the sol-gel technique. The dehydration process shows two well-defined stages. The analysis of the dynamics allows the analysis of the mode in which water is released from the material. The relationship with the degradation of the organic matrix and phase transitions due to the thermal treatment are discussed. Experimental The experimental setup is shown in Figure 1, it consisted of a laser (He-Ne 20 mW) whose light, which is mechanically modulated by a chopper (Stanford Research 540) at a constant frequency (f = 7 Hz) for all experiments (e). The laser was focused over the reference material (c) (aluminum foil of 50 μm thickness) with a thermal diffusivity of 0.9 cm2/s through a quartz window (d), both of them are sealing the photoacoustic (PA) cell with vacuum grease. The emulsions samples (a) of interest were placed inside a 1 mm thick acrylic ring (b) on the external surface of the reference material. A commercial electret microphone was used (f), this microphone signal is fed into a lock-in amplifier (Stanford Research 830), from where the output signal amplitude is recorded, as a function of time, in a personal computer. In this configuration the PA cell is closed. |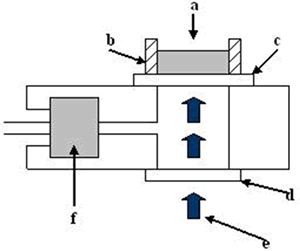 
| | Figure 1. Schematic arrangement of the conventional PA cell. The sample (a) is contained in an acrylic ring (b). The laser (e) passes through the window (d) and impinges on the reference material (c) and the signal is detected with a microphone (f). | The samples to be studied were prepared mixing 2:1 (wt.%) of water and powdered sample. The mixture was homogenized during 30 minutes in an ultrasonic bath and an emulsion was obtained. All experiments were performed at constant room temperature. The titania samples in powder form received a previous thermal treatment from ambient temperature up to 700oC during 12 h. The crystalline phases were determined by X-ray diffraction (XRD) technique using a Siemens D-5000 diffractometer with a CuKα radiation. Long annealing treatments were made in order to study phase crystallization. The powder samples were placed in platinum crucibles and heated at 120, 350, 550 and 700°C, during 12 h. The XRD patterns were registered in the range 5-60° 2θ with a step size of 0.02° and a step time of 2 s. Theory According to the Rosencwaig and Gersho model [22], the PA signal is determined by the temperature fluctuation (θ) at the air-substrate interface. Solving the thermal diffusion equations for this configuration this temperature can be determined  (1)
l is the thickness of the reference material or substrate, σ is the complex thermal diffusion coefficient, defined by  , with a=(πf/α)1/2, and b=εb/ε is the thermal coupling coefficient, with ε and εb the thermal effusivities of the substrate and sample, respectively. θ0 is the expression for the temperature fluctuation in the absence of the sample on the substrate, which is given by θ0= (I0/2kσ) coth(σ l). In arriving to equation (1), it has been taken into account that the effusivity of air (εair=5.6x10-4Ws1/2 /cm2 K) is much smaller than the thermal effusivity of the aluminum substrate (ε=2.4 Ws1/2 /cm2 K). Since the substrate is optically opaque, it has been considered that the optical absorption coefficient, β, is much larger than the absolute value of the complex thermal diffusion coefficient, |σ|, for the used frequency. Moreover, the sample thickness, lb, is much larger than its thermal diffusion length, which is given by µb = (αb/πf )1/2, being αb the thermal diffusivity of the sample. From equation (1) the amplitude of the ratio θ/θ0 is given by  (2)
Solving Eq. (2) for the thermal coupling coefficient b, the thermal effusivity of the emulsion can be obtained as a function of time, this is.  (3)
where A = (q2 - 1)[cosh2(2x) + cos2(2x)] + 2 (q2 + 1)cosh(2x) cos(2x), B = sinh(2x)[(q2 - 1)cosh(2x) + (q2 + 1)cos(2x)], C = (q2 - 1)[cosh2(2x) + cos2(2x)], and x = al. Measuring the evolution of q = q(t), the values of εb(t) can be obtained. Thermal effusivity (ε) is a highly relevant quantity when studying time-varying problems and it is related to the heat capacity per unit volume (ρC) and to the thermal conductivity (k) by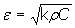 
This property evaluates the heat interchange between the sample and the surrounding medium. In the case of a semi-infinite material at temperature T0, which is placed in contact with a reservoir at a higher temperature (T), the heat flow at a given time (t) is given by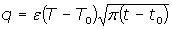 
with t0 the initial time. In other words the heat flow is proportional to the thermal effusivity for time varying conditions[23]. Results and Discussions The results of the thermal effusivity as a function of time of samples that received a prior thermal treatment from ambient temperature to 700oC are presented in Figure 2. During the dehydration process, thermal effusivity showed two sigmoidal decay stages as a function of time. Each of them was fitted with a sigmoidal curve, therefore a double sigmoidal fitting functions is used to analyze the experimental data [12]:  (4)
| 
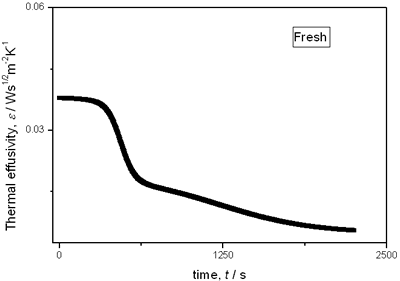
(a)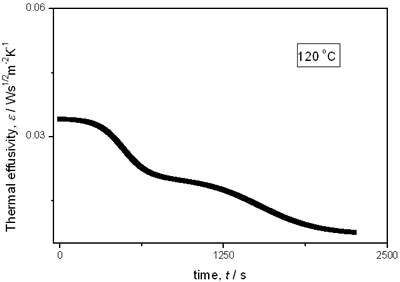 
(b)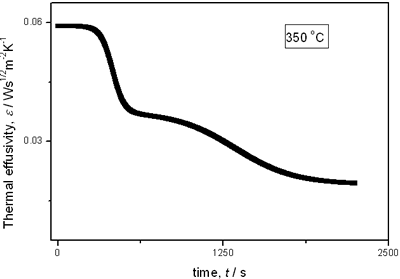 
(c)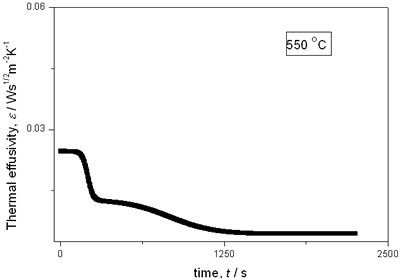 
(d)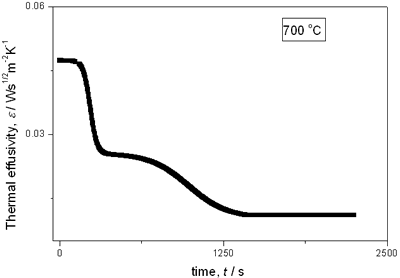 
(e) | | Figure 2. Thermal effusivity as a function of time of samples that received a previous thermal treatment from room temperature up to 700ºC: a) fresh sample; b) 120ºC; c) 350ºC; d) 550ºC; e) 700ºC. | The different time interval obtained from the parameters of the logistic curves as a function of temperature are shown in Figure 3. These results indicate that the annealing treatment strongly affects the dehydration process. In the first stage the dehydration time, t0, (Figure 3a) increases almost linearly, and in the second stage, the similar parameter, tp (Figure 3b) also increases progressively, presenting an inflexion in the interval 200°C to 400°C. This inflexion also appears in the time t0, although in this case, it is smaller. |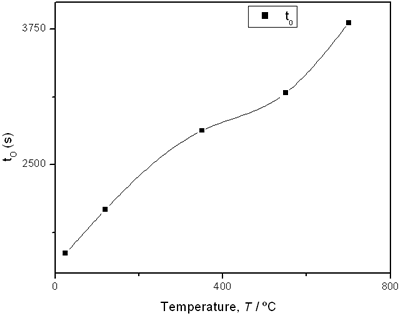 
(a)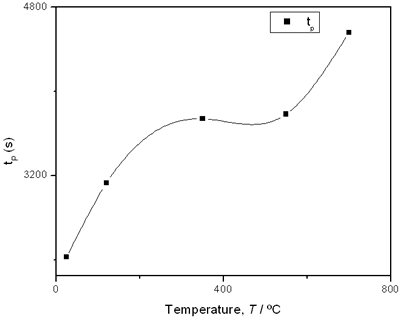 
(b)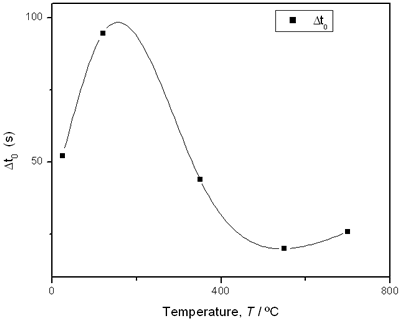 
(c)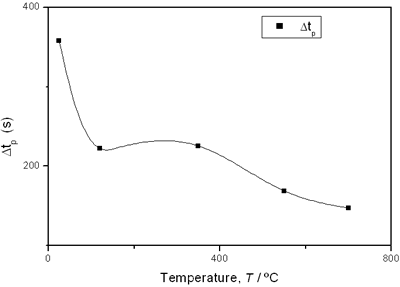 
(d) | | Figure 3. Time intervals obtained from the parameters of the logistic curves as a function of temperature: a) and b) t0 and tp are the time intervals when each sigmoidal process reaches its maximum derivative. c) and d) Δt0 and Δtp are the mean times in which each sigmoidal growth process occurs. | On the other hand, for the settle down time, or the time at which the process takes place within a thermal diffusion length, a different behavior is observed (Figure 3, c and d). In the first stage, the time interval Δt0 shows a maximum for temperatures around 200ºC and after that a strong decrease is observed. In the case of the settle down time in the second stage Δtp a constant decrease is observed with certain stabilization around 300ºC. The two-stages dehydration process indicates two modalities of releasing water in the process, the first process would involve, water not strongly bound to the structure of the sol-gel matrix with titania. The inflexions around 350ºC for the time intervals t0, tp and Δtp (Figures 3a, b, d) can be related to the degradation of the organic matrix due to the thermal treatments, affecting both stages of dehydration. The systematic degradation of the organic matrix would also explain the fact that the settle down times Δt0 and Δtp (Figures 3c, d) are shorter when the temperature increases, indicating a higher dehydration velocity. The increments in the time intervals t0, tp indicate a delay in the detection of the process inside of a thermal diffusion length. This time is affected by the thermal diffusivity of the mixture titania-water. A third factor influencing the behavior of these results would appear at higher temperatures where a phase transition from anatase to rutile is present. This has also been confirmed by X-ray diffraction (Figure 4). Initially the X-ray diffractograms exhibit the formation of wide peaks with a low crystalline pattern which corresponds to anatase phase, however increasing the temperature a sharp and well defined peaks are observed at 550°C, even at higher values of 2θ whereas double reflections are observed at 37, 55 and 70 (2θ). At 700°C the appearance of small reflections related to rutile, the high temperature form of titania, are detected at 27.6, 36.3, 41.5, and 57.0 (2θ). The behavior of the dehydration curves above 500ºC is affected and could be related with the increase in intervals the time intervals t0, tp and Δt0 |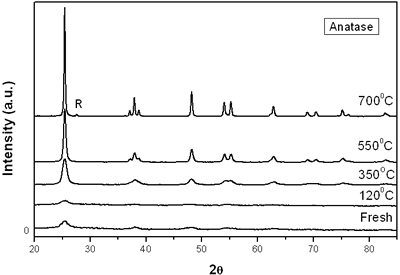 
| | Figure 4. X-ray diffraction of titania treated at different annealing temperature. R = Rutile. | Conclusions The dehydration of aqueous emulsions of powdered titania obtained by the sol-gel method and thermally treated from room temperature up to 700ºC, was monitored using photoacoustic spectroscopy. It is shown that using a modified conventional photoacoustic cell, the thermal effusivity can be determined as a function of time during the dehydration process. The results indicate that thermal effusivity follows a two-stage process each of them can be fitted by a second order kinetics. The analysis of the curves provided us the dehydration time and settle down time. The behavior of this time intervals is strongly influenced by the degradation of the organic material due to the thermal treatment. The contribution of the phase transition from anatase to rutile was discussed as well as the influence of the thermal diffusion length due to the differences in thermal diffusion inside the sample. Our results indicate that even though, the dehydration process is very complex; this technique could provide us with useful results with interesting perspectives not only on the comprehension of the process but in the performance and application of similar materials. Acknowledgements The authors wish to thank Eng. J. Bante-Guerra for assistance in the electronics and M.Sc. D. H. Aguilar for the X-ray diffraction. This work was partially supported by Conacyt project 38493-U. References 1. C. Garzella, E. Comini, E. Tempesti, C. Frigeri and G. Sberveglieri, “TiO2 thin films by a novel sol-gel processing for gas sensor applications”, Sensors Actuators B, 68 (2000)189-196. 2. A. Fujishima, T. Rao and D.Tryk, “Titanium dioxide photocatalysis”, Photochem. Photobiol. C, 1 (2000) 1-21. 3. M. Gratzel, “Semiconductor Nanoclusters-Physical”, Chemical and Catalytic Aspects, Ed. P V Kamat and D Meisel (Amsterdam: Elsevier) (1997) pp 353-461. 4. K. Rao, M. Murthy and S. Mohan, “Optical properties of electron beam evaporated TiO2”, Thin Solid Films, 176 (1989) 181-186. 5. S. Mo and W. Ching, “Electronic and optical properties of three phases of titanium dioxide: rutile, anatase and brookite”, Phys. Rev. B, 51 (1995) 13023-13032. 6. P. Gouma and M. Mills, “Anatase to Rutile Transformation in Powders of Titania”, J. Am. Ceram. Soc., 84 (1995) 619-622. 7. P. Lottici, D. Bersani, M. Braghini and A. Montenero, “Raman scattering characterization of gel-derived titania glass”, J. Mater. Sci., 28 (1993) 177-183. 8. M. Suhail, Rao Mohan and S. Mohan, “DC reactive magnetron sputtering of titanium-structural and optical characterization of TiO2 films”, J. Appl. Phys., 71 (1992) 1421-1427. 9. K. Kumar, K. Keizer, A. Burggraf, T. Okubo, H. Nagamoto and S. Morooka, “Densification of nanostructured titania assisted by a phase transformation”, Nature, 358 (1992) 48-51. 10. S. Liao, W. Mayo and K. Pae, “Synchrotron Radiation Investigation of Thermal Stability and Grain-Growth in Pure and Metal-Doped Nanocrystalline TiO2”, Acta. Mater., 45 (1997) 4027-4040. 11. D. Bersani, G. Antonioli, P. Lottici and T. Lopez, “Raman study of nanosized titania prepared by sol–gel route”, J. Non-Cryst. Solids, 175 (1998) 232-234. 12. M. Vargas-Luna, G. Gutierrez-Juarez, J. R. Rodríguez-Vizcaino, J. B. Varela-Najera, J. M. Rodríguez-Palencia, J. Bernal-Alvarado, M. Sosa and J. J. Alvarado-Gil, “Photoacoustic monitoring of inhomogeneous curing processes in polystyrene emulsions”, J. Physics D: Appl. Phys., 35 (2002)1532-1537. 13. A. G. Bell, “Upon the Production of Sound by Radiant Energy “, Philos. Mag., 11 (1881) 510-528. 14. A. Rosencwaig, Opt. Commun., 7 (1973) 305-308. 15. C. Manfredotti, F. Fizzotti, M. Boero and M.C. Bossi, “Determination of the absolute optical absorption coefficient for thermally thick samples by photoacoustic spectroscopy”, Solid State Commun., 98 (1996) 655-659. 16. M. V. Marquezini, N. Cella, A. M. Mansanares, H. Vargas and L. C. M. Miranda, “Open photoacoustic cell spectroscopy”, Meas. Sci. Technol., 2 (1991) 396-401. 17. A. Pinto Neto, H. Vargas, N. F. Leite and L. C. M. Miranda, “Photoacoustic investigation of semiconductors: influence of carrier diffusion and recombination in PbTe and Si”, Phys. Rev. B, 40 (1989) 3924-3930. 18. O. Pessoa, Jr., C. L. Cesar, N. A. Patel, H. Vargas, C. Guizoni, L. C. M. Miranda. “Two-beam photoacoustic phase measurement of the thermal diffusivity of solids”, J. Appl. Phys., 59 (1986) 1316-1318. 19. N. F. Leite, N. Cella and H. Vargas, “Photoacoustic measurement of thermal diffusivity of polymer foils”, J. Appl. Phys., 61 (1987) 3025-3027. 20. J. A. Balderas-López, G. Gutiérrez-Juárez, M. Fonseca-Jaime and F Sánchez-Sinencio, “Measurements of thermal effusivity of liquids using a conventional photoacoustic cell”, Rev. Sci. Instrum., 70 (1999) 2069-2071. 21. T. López, M. Picquart, G. Aguirre, G. Arriola, Y. Freile, D. H. Aguilar, P. Quintana, J. J. Alvarado-Gil and F.M. Vargas-Luna, “Thermal Characterization of Agar Encapsulated in TiO2 SOL-GEL”, Int. J. Thermophys., 25 (2004) 1483-1493. 22. A. Rosencwaig and A. Gersho, “Photoacoustics and Photoacoustic Spectroscopy”, J. Appl. Phys., 47 (1976) 64-69. 23. Agustín Salazar, “On thermal diffusivity”, Eur. J. Phys., 24 (2003) 351-358. Contact Details |