Psylotech Inc. will have an all new 3D Dynamic Mechanical Analyzer (DMA) on display at Pittcon in Orlando, FL, March 12-15, 2012. Psylotech's DMA is a universal testing machine specially purposed to measure the mechanical properties of structural plastics, enabling precise, accurate finite element analysis of viscoelastic materials.
The all new 3D Dynamic Mechanical Analyzer (DMA) from Psylotech.
It is the first instrument of its kind to offer:
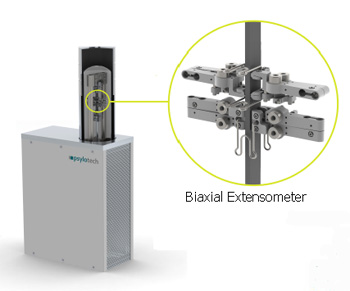
- Local Strain Measurement on axially loaded specimens circumvents the substantial experimental errors associated with traditional beam bending specimens.
- Dynamic Poisson's Ratio ( n * ) plus Young's Modulus ( E *) are concurrently measured, enabling determination of a viscoelastic material's full 3D mechanical property matrix.
- Time domain moduli in an FEA compatible format . Psylotech also provides software modules to leverage the data in commercial finite element codes, simplifying adoption into the product development process.
The Viscoelastic Modeling Process The mechanical properties of polymers depend on rate, history, temperature, pressure, solvent absorption, and internal damage. Psylotech's DMA uses advanced reduced time constitutive models proven in the literature and powerful enough to quantify this complicated behavior. A reliable polymer constitutive model enables effective simulations in commercial FEA software such as Abaqus, Ansys, etc. to streamline polymer recipe customization, accelerate product development, and improve quality.
Dynamic Poisson's Ratio The 3D DMA measures Dynamic Poisson's ratio (n*) concurrently with dynamic Young's Modulus (E*). The power of this simultaneous property measurement lies in the capability of inferring a material's full 3D mechanical property matrix. And since both properties are measured on the same sample that experiences the same temperature, strain and processing history, the resulting data set is uniquely selfconsistent. The net result is a paradigm shift for time-dependent, viscoelastic material simulations.
Traditional beam bending specimens produce only E* and presume a constant Poisson's ratio from glassy through rubbery material behavior.. This assumption leads to significant errors when modeling dilatation strains, as is evident by comparing viscoelastic bulk modulus inferred from E' plus constant and measured Poisson's ratio (see plot). It is well known that Bulk modulus remains relatively constant over a material's frequency response, similar to the red curve. Ignoring dynamic Poisson's ratio gives a 10x fluctuation over the frequency range, implying 10x error in the dilatational component of an FEA model.