Oct 24 2017
Consider wriggling worms covering a small donut-shaped droplet, where the worms are so tightly packed that they are pressurized to locally line up corresponding to one another. In such a case, we expect the worms to form a nematic liquid crystal, that is, an ordered phase like the materials used in various flat panel displays.
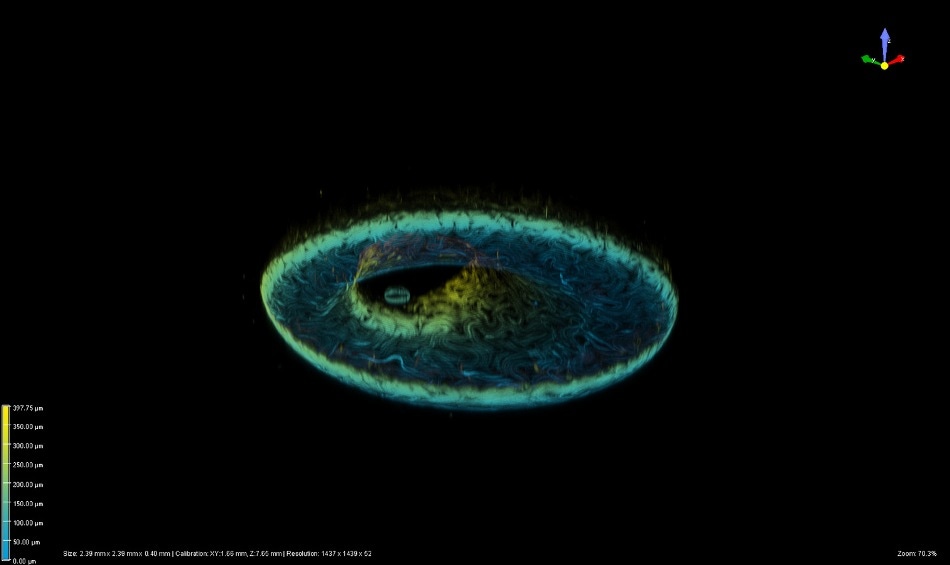 Image taken with a confocal microscope of a toroidal structure, false-colored by height. The worm-like structures are microtubules driven by kinesin motor proteins. CREDIT: Perry Ellis, Georgia Tech.
Image taken with a confocal microscope of a toroidal structure, false-colored by height. The worm-like structures are microtubules driven by kinesin motor proteins. CREDIT: Perry Ellis, Georgia Tech.
In contrast, the nematic phase created by the worms constitutes very small regions in which the local alignment is lost, which are the flaws in the otherwise aligned material. Moreover, as the worms move constantly and alter their configuration, the nematic phase is active and nowhere close to equilibrium.
In the study published in the Nature Physics journal on October 23rd, 2017, Researchers from the Georgia Institute of Technology and Leiden University in The Netherlands have given a detailed account of the outcomes of an integrated theoretical and experimental investigation of an active nematic on the surface of donut-shaped, or toroidal, droplets. Yet, the Scientists did not employ actual worms. In contrast, they used an active nematic formed of flexible filaments enclosed by microscopic engines that constantly convert energy into motion.
This specific active material, initially designed at Brandeis University, adopts cellular machinery elements, including kinesin motor proteins functioning as the engines, rod-like microtubule bundles that form the filaments, and ATP as the fuel. Integration of this activity with flaws makes the flaws active and traveling around similar to swimming microorganisms to explore space, here they explore the toroidal droplet surface.
The Researchers analyzed the toroidal droplets covered by the active nematic and validated a long-established theoretical prediction related to liquid crystals at the state of equilibrium—initially debated by Bowick, Nelson and Travesset—that nematic flaws on the droplets’ curved surface is sensitive to the local curvature. Yet, as the active nematic adopted in this study is nowhere closer to equilibrium, the team also discovered the way the internal activity changed and enhanced the anticipations.
There have been predictions that say defects are very sensitive to the space they inhabit, specifically to the curvature of the space. The torus is a great place to investigate this because the outside of the torus, the part that looks locally like a sphere, has positive curvature while the inner part of a torus, the part that looks like a saddle, has negative curvature.
Perry Ellis, Graduate Student, School of Physics, Georgia Tech and the First Author of the paper
“The quantity that characterizes a defect is what we call its topological charge or winding number,” stated Alberto Fernandez-Nieves, a Professor in Georgia Tech’s School of Physics and another Co-Author of the paper. “It expresses how the alignment direction of the nematic liquid crystal changes as we go around the defect. This topological charge is quantized, meaning that it can only take values from a discrete set that are multiples of one-half.”
In the experiments performed, the topological charge of each flaw was +1/2 or -1/2. In order to ascertain the location and charge of each flaw, Ellis scrutinized the toroidal droplets over time by means of a confocal microscope and then investigated the resulting video by adopting methods acquired from computer vision. The Scientists discovered that although the molecular motors drove the system far from equilibrium, the flaws could still sense the curvature, where the +1/2 defects migrated toward the positive curvature region and the -1/2 defects migrated toward the negative curvature region.
In this latest study, the Researchers went one step closer to gaining an in-depth knowledge of the ways to control and lead flaws in an ordered material.
We have learned that we can control and guide partially ordered active matter using the curvature of the underlying substrate. This work opens opportunities to study how the defects in these materials arrange on surfaces that do not have constant curvature. This opens the door for controlling active matter using curvature.
Alberto Fernandez-Nieves, Professor, School of Physics, Georgia Tech and another Co-Author of the paper
An unanticipated outcome of the research was that the constant movement of the flaws renders the average topological charge to be continuous, and not considering only values that are multiples of 1/2.
“In the active limit of our experiments, we found that the topological charge becomes a continuous variable that can now take on any value,” stated Fernandez-Nieves. “This is reminiscent of what happens to many quantum systems at high temperature, where the quantum, discrete nature of the accessible states and associated variables is lost. Instead of being characterized by quantized properties, the system becomes characterized by continuum properties.”
Ellis’ scrutiny of the droplets was in correspondence with the numerical simulations performed by Assistant Professor Luca Giomi and Postdoctoral Researcher Daniel Pearce at the Instituut-Lorentz for Theoretical Physics at the Universiteit Leiden in The Netherlands.
Our theoretical model helped us decipher the experimental results and fully understand the physical mechanism governing defect motion, but also allowed us to go beyond the current experimental evidence.” Giomi added that “Activity changes the nature of the interaction between defects and curvature. In weakly active systems, defects are attracted by regions of like-sign Gaussian curvature. But in strongly active systems, this effect becomes less relevant and defects behave as persistent random-walkers confined in a closed and inhomogeneous space.
Daniel Pearce, Postdoctoral Researcher , The Instituut-Lorentz for Theoretical Physics, The Universiteit Leiden, The Netherlands
There are various active system examples guided by internal activity, such as bird flocks, traffic flows, swimming microorganisms and robot swarms. “Active materials are everywhere, so our results aren’t limited to just this system on a torus,” further stated Ellis. “You could see the same behavior in any active system with defects.”
The study opens the door for further research on active fluids. “Our results introduce a new framework to explore the mechanical properties of active fluids and suggest that partially ordered active matter can be guided and controlled via gradients in the intrinsic geometry of the underlying substrate,” noted the Authors in a summary of the paper.
The National Science Foundation (under award 1609841) and the Netherlands Organization for Scientific Research supported the study. The findings, opinions and conclusions or recommendations conveyed in this article are those of the authors and do not compulsorily echo the opinions of the sponsoring agencies.