Jul 30 2018
Atoms arranged mutually in crystal space are believed to correlate with the least of the potential energy of interaction of all crystal atoms.
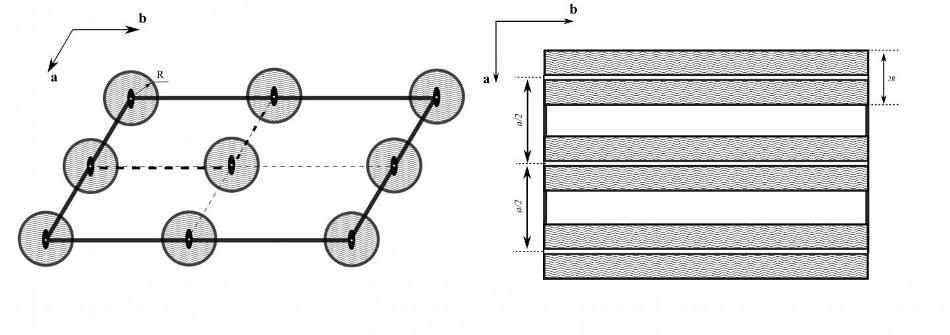 Fig. 1. Forbidden volume in two-dimensional space symmetry groups: (left) p2 and (right) pm. Wavy filling indicates forbidden regions.(Image credit: Lobachevsky University
Fig. 1. Forbidden volume in two-dimensional space symmetry groups: (left) p2 and (right) pm. Wavy filling indicates forbidden regions.(Image credit: Lobachevsky University
For rough description of the arrangement of atoms in crystals, the principle of potential energy minimum can be applied in several geometric ways. Particular, these geometric ways comprise of the principle of proximal packing of molecules for molecular crystals and the principle of proximal packing for crystals of inorganic compounds with undirected bonds.
At the Department of Crystallography and Experimental Physics of the Lobachevsky University, researchers believe that when examining the possibility of applying a particular space group as a crystal symmetry group, it is important to account for the following key factors—the shape and volume of the part of crystal space where molecules or ions can be located, and also the molecular symmetry (owing to the presence of regular systems of points at which the atoms of a specified molecule can be located).
"If one considers atoms as geometric objects, which have a finite volume comparable with the volume of a crystal unit cell, it is necessary to consider the geometric limitations on the mutual arrangement of atoms in crystal space. These limitations are due to the fact that the distance between two atoms cannot be smaller than the sum of their crystallochemical radii," comments Evgeny Chuprunov, Head of the Department of Crystallography and Experimental Physics, and Rector of the Lobachevsky University.
All of the 230 symmetry space groups are defined by specific constraints on the arrangement of atoms in crystal space, which are established by the group of elements of space group symmetry, and also the sizes of unit cells. That is, for purely geometric reasons¸ certain regular systems of points of these groups cannot occur in nature. The set of these points results in "forbidden regions" in crystal space, and the occurrence of such regions was shown by Mikhail Porai-Koshits, the remarkable chemist and crystallographer, and laureate of the Chugaev Prize.
We have determined the symmetry of forbidden regions for packing solid circles in a two-dimensional space, whose symmetry is described by one of two-dimensional space symmetry groups. It was also established that, depending on the symmetry of forbidden regions, two-dimensional space symmetry groups can be divided into seven classes.
Nikolai Somov, Associate Professor of the UNN Department of Crystallography and Experimental Physics
Lobachevsky University researchers determined the symmetry of forbidden regions for packing solid spheres in the three-dimensional crystal space of varying symmetry. In this context, 33 classes of spatial symmetry of forbidden regions characterized the 230 space symmetry groups, according to the results achieved.
"The approach proposed here can be generalized for the case of n-dimensional spaces of larger dimension and packing of elements of a more complex shape," concludes Evgeny Chuprunov.