Jan 8 2019
Synchronization can be observed when two diverse systems oscillate in an identical way. This underlies many collective phenomena seen in nature, providing an example for emergent behaviors spanning from the acoustic harmony of cricket choruses to the behavior of the human brain.
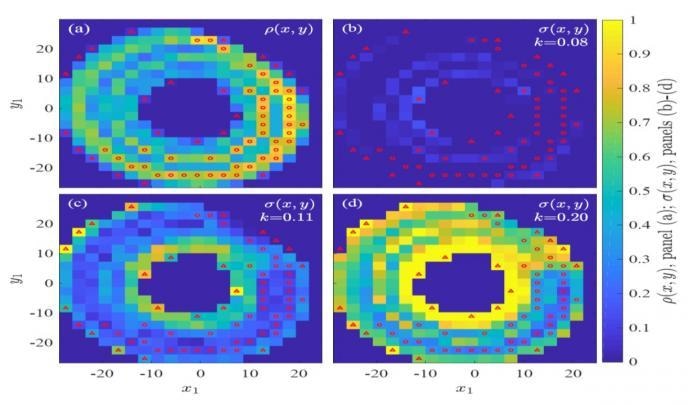These shapes of donuts are the global structures of the Rossler system (named Rossler attractors). The colored points are the local synchronizations that emerged between the systems in different coupling strengths. (Image credit - Nir Lahav)
Would it also be possible for chaotic systems to synchronize with each other? How do synchronization and self-organization emerge from systems that did not possess these properties to start with? Characterizing and appreciating the transition from disorder to synchrony is of central importance in comprehending the emergence of synchronization and self-organization in nature.
In a new research published in Physical Review E, physicists from Bar-Ilan University in Israel, together with colleagues from India, Spain, and Italy, examined the Rossler system, a popular chaotic system which physicists have explored methodically for nearly four decades. Looking at this system from a new standpoint, they discovered new phenomena that have been unnoticed until now.
For the first time, the scientists could measure the fine grain process that leads from disorder to synchrony, discerning a new kind of synchronization between chaotic systems. They term this new phenomenon Topological Synchronization. Traditionally, synchronization has been studied by comparing the time-course of activity of the two systems. Topological Synchronization instead analyzes synchronization by equating the structures of the systems. The chaotic system is thus inspected at the level of its structure, adopting a more global approach to establish the process of synchronization.
Chaotic systems, although unpredictable, still have a subtle global organization called strange attractor. Every chaotic system attracts its own unique strange attractor. By Topological Synchronization we mean that two strange attractors have the same organization and structures. At the beginning of the synchronization process, small areas on one strange attractor have the same structure of the other attractor, meaning that they are already synced to the other attractor. At the end of the process, all the areas of one strange attractor will have the structure of the other and complete Topological Synchronization has been reached.
Nir Lahav, Study Lead Author, Department of Physics, Bar-Ilan University
The discovery of Topological Synchronization exposes that, in contrast to what was formerly assumed, chaotic systems synchronize slowly through local structures that, unexpectedly, kick off in the sparse areas of the system and only then spread to the more populated areas. In these sparse areas, the activity is less chaotic compared to other areas and, consequently, it is easier for these areas to sync relative to those that are a lot more unpredictable.
In order to understand why this is surprising, think of this scenario: two groups of friends meet at a party. In every group, we can find extroverts, who easily connect with strangers, and introverts, who find it harder to connect with a new group. We would assume that the first connections would occur between the extroverts and only later would the introverts create connections. It would be very surprising to see this happen the other way around. But this is exactly what we found in our results. We assumed that the dense areas of the system, where most of the activity is, would sync with each other first (like the extroverts), but in reality, we discovered that the low-density areas were the first to sync (the introverts).
Nir Lahav, Study Lead Author, Department of Physics, Bar-Ilan University
This conceptual uniqueness relates not only to the core understanding of synchronization, but also carries direct practical inferences on the predictability limits of chaotic systems. Indeed, on account of this newly-defined local synchronization, the scientists demonstrate that the state of one system can be inferred from measurements of the other, even in the nonexistence of universal synchrony. It is possible to predict where synchronized areas will appear in weak coupling, much before full synchronization.
The scientists are presently applying their findings to try to expose how self-organization may emerge in other complex systems in nature such as the human brain.