Introduction Recently, the importance of optical information processing has been increasing. Optical encryption techniques on information security were proposed and has been studied [1]. The optical image wavelet transform is an efficient tool for the processing in both time and frequency domain [2]. Holographic data storage has received more attention because of its high storage capacity at high speed [3]. Holography is one of the main techniques which allows the registration, transformation, and manipulation of the spatial structure of the light wave fronts. Previous publications have demonstrated that the edge enhancement and the spatial frequency filtering of two-dimensional optical image in a photorefractive mesogenic composites film with Fourier transform holography [4, 5]. Because of its good optical properties, our photorefractive mesogenic composites film was used as the dynamic holographic medium in the experiments. Photorefractive effect is a well-known phenomenon in which the refractive index of materials is spatially modulated due to the photoinduced redistribution of charges. The redistribution of charges induces a space-charge field, which subsequently modulates the refractive index via an electro-optic effect. Consequently, in a photorefractive liquid crystal, refractive index modulation (hologram) is produced by reorientation of liquid crystal molecules [6]. In this paper we present a matched filter technique which allows the spatial correlation of two optical images for pattern classification and/or detection. Experimental Our photorefractive material consists of low-molar-mass liquid crystal (E7), functionalized copolymer synthesized by free radical copolymerization of methacrylate monomers containing 4-cyanobenzoate and N-ethylcarbazoyl side groups, and photoconductive sensitizer 2,4,7-trinitro-9-fluorene (TNF) in a 78:20:2 weight ratio (Figure 1). The composite was sandwiched between two glass slides coated with indium tin oxide. The thickness of the sample, as controlled by spacers, was 50 μm. In the sample, liquid crystals aligned very stable homeotropic state at room temperature [7]. We performed the experiment of two-dimensional optical image correlation by means of conventional matched filtering technique by using Fourier transform holography as shown in Figure 2 [5]. Two Fourier-transformed imaging beams, “Original image” and “Reference image” generated by mask1 and mask2, respectively. The imaging beams are p-polarized and derived from He-Ne laser (633 nm), and intersected at 0.8 degree. The sample placed in the superposition of two beams and tilted by 45 degree with respect to the beam bisector. Grating spacing was 18 μm (in the Raman-Nath regime) and an applied dc voltage of 0.16 V/μm. In this work, we observed first order self-diffraction in order to evaluate the spatial correlation. | 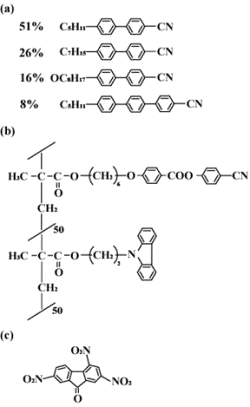
| | Figure 1. Chemical structures of the photorefractive mesogenic composite. (a) low-molar-mass liquid crystal, (b) functionalized copolymer, and (c) photoconductive sensitizer (TNF). | | 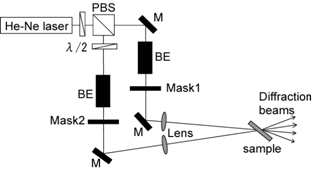
| | Figure 2. Experimental setup. M: mirror, BE: beam expander, PBS: polarization beam splitter, and λ/2: half wave plate. | Results and Discussion Figure 3 presents experimental results of the optical image correlation when the optical images of Arabic numerals character “1”, “2”, and “3” were used as an example pattern. The pictures of “Reconstructed images” in Figure 3 show correlation output of the used reference images “1” and “2”, respectively. It is obvious that the image correlation exists between the “Original image” and the “Reference images”. Differences between input optical images generated by photomask and reconstructed images are probably caused by the quality of the used photomask. Small discrepancies of spatial frequency of input images influence the performance of the correlation output. In fact, a visual inspection of the reconstructed images shows a very poor image quality with respect to their edges. This construction technique is very sensitive to the adjustment of the overlapping between two imaging beams with respect to the focal plane of the Fourier transform lens. | 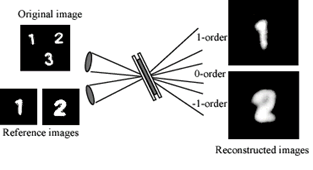
| | Figure 3. Correlation results between the “Original image” and the “Reference images”. | The resulting correlation output can be described by the convolution theorem [8, 9]. The Fourier transformed electric field of two input optical images e1(x,y) and e2(x,y) are expressed in the back focal plane where the sample plane is situated  (1) (1)
 (2) (2)
The intensity which describes the hologram in the focal plane is given by  (3) (3)
Finally, the reconstructed images are given by performing the inverse Fourier transform of Eq. (3).  (4) (4)
where l is the distance between two input images in the xy-plane, e1*(x,y) and e2*(x,y) denote the complex conjugation of e1*(x,y) and e2*(x,y), respectively. In Eq. (4), the third and fourth terms are equivalent to the following convolution theorem.  (5) (5)
Thus, this expression presents the experimental results of the reconstructed images. Conclusions Two-dimensional optical image correlation by using conventional Fourier transform holography in a photorefractive mesogenic composite film was observed. It was possible to recognize correlation images such as Arabic numerals. The theoretical descriptions are given by the well-known convolution theorem. Acknowledgements This work was partially supported by the 21st Century COE program and a Grant-in-Aid for Scientific Research from the Ministry of Education, Science, and Culture of Japan. We also thank Japan Chemical Innovation Institute for supporting our study. References 1. R. Arizaga, R. Henao and R. Torroba, “Fully Digital Encryption Technique”, Opt. Commun., 221 (2003) 43-47. 2. H. Zhang, C. M. Cartwright, M. S. Ding and W. A. Gillespie, “Image Feature Extraction with Various Wavelet Functions in a Photorefractive Joint Transform Correlator”, Opt. Commun., 185 (2000) 277-284. 3. J. Ashley, C. M. Jefferson, M.-P. Bernal, B. Marcus, G. W. Burr, R. M. Macfarlane, H. Coufal, R. M. Shelby, H. Guenther, G. T. Sincerbox and J. A. Hoffnagle, “Holographic Data Storage”, IBM J. Res. Develop., 44 (2000) 341-368. 4. H. Ono, T. Kawamura, N. Kawatsuki and H. Norisada, “Intensity Filtering of a Two-dimensional Optical Image in High-performance Photorefractive Mesogenic Composites”, Appl. Phys. Lett., 79 (2001) 895-897. 5. A. Emoto, H. Ono and N. Kawatsuki, “Spatial Frequency Selective Reconstruction using Fourier Transform Holograms Generated in Functionalized Mesogenic Composites”, Liq. Cryst., 30 (2003) 1201-1206. 6. G. P. Wiederrecht, “Photorefractive Liquid Crystals”, Annu. Rev. Mater. Res., 31 (2001) 139-169. 7. H. Ono, T. Kawamura, N. M. Frias, K. Kitamura, N. Kawatsuki, H. Norisada and T. Yamamoto, “Holographic Bragg Grating Generation in Photorefractive Polymer-dissolved Liquid-crystal Composites”, J. Appl. Phys., 88 (2000) 3853-3858. 8. F. E. Terman, “Introduction to Fourier Optics”, (McGraw-Hill, 1968) 210-214. 9. B. Fleck, L. Wenke, P. S. Ramanujam and S. Hvilsted, “Theoretical and Experimental Investigations on an Incoherent Optical Correlator”, Opt. Commun., 174 (2000) 311-315. Contact Details |