Sponsored by HORIBAJun 14 2018
When polarized light is incident on a prism covered by a thin layer of metal, a phenomenon called surface plasmon resonance (SPR) occurs. This is an optical detection technique that depends upon the absorption of photons in an incident light beam by free electrons on the metallic surface of the prism, called the SPRi-Biochip, under appropriate conditions of wavelength, polarization and angle of incidence.
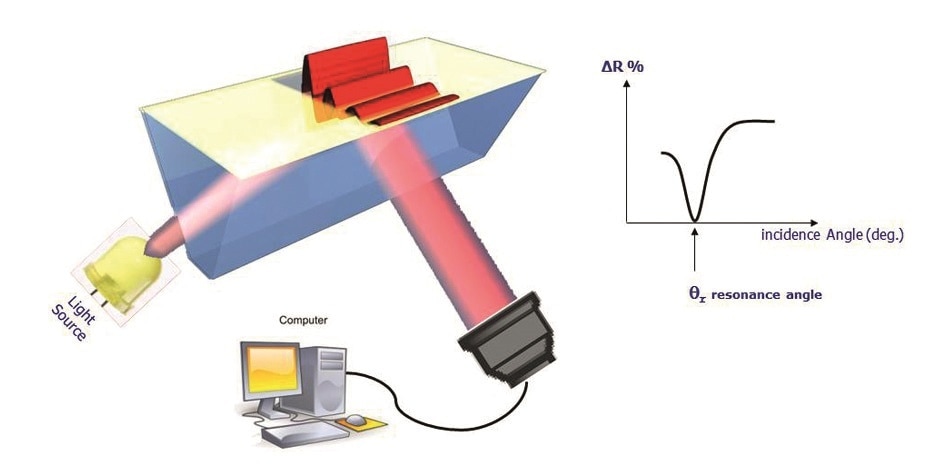
Figure 1. SPRi configuration.
The result is the conversion of photons into surface plasmon waves, which penetrate the overlying medium for about 100-200 nm. When the angle of incidence is just right, the plasmon waves show resonance with the incident photons, leading to a sudden fall in reflectivity. This angle is called the resonance angle. The plasmon curves thus mirror the changes in the reflected light which is acquired by the camera, plotted against the angle of incidence.
The resonance angle varies in position, being specific to the immediate environment of the surface of the SPRi-Biochip. The surface of the SPRI-Biochip can be modified at about 200 nm to produce this type of measurable change in resonance conditions, such as by forming a different ligand-analyte complex.
What is a Plasmon?
A plasmon is the specific physical occurrence that is known to accompany plasma oscillation. In other words, physics defines plasmons as quanta of plasma oscillation just as photons are quantified light waves. A plasmon is thus a quasi-particle, and can be coupled with a photon to generate a plasma polariton, another quasi-particle. Plasmons are considered collective oscillations of the density of free electron gas, often following the frequencies of light.
What is a Surface Plasmon?
While plasmons are collective gas density oscillations, surface plasmons represent collective oscillations of the free electron cloud of the metal surface. They may be better considered as plasmons that are limited to the surface and interact strongly with photons to form a surface plasma polariton, or a surface plasmon wave.
Why Perform Imaging?

Figure 2. Flow cell image (left) and difference image (right).
In order to monitor all the resonance conditions existing on the SPRi-Biochip surface at the same time, imaging is used. The use of a variety of molecules (“ligands” or “spots”) immobilized in array format allows the parallel monitoring of potential interactions between them with a camera. This ability to measure all the array elements simultaneously is termed multiplexing.
It is made possible by the use of the inbuilt imaging feature in all SPRi devices, that covers the measurement of several hundred biomolecular interactions at the same moment. The software retrieves the image of the flow cell that reflects the SPRi-Biochip surface image in real time. A difference image displays the interacting elements as spots following the analyte solution injection.
What are the Different Phases of a Kinetic Curve?
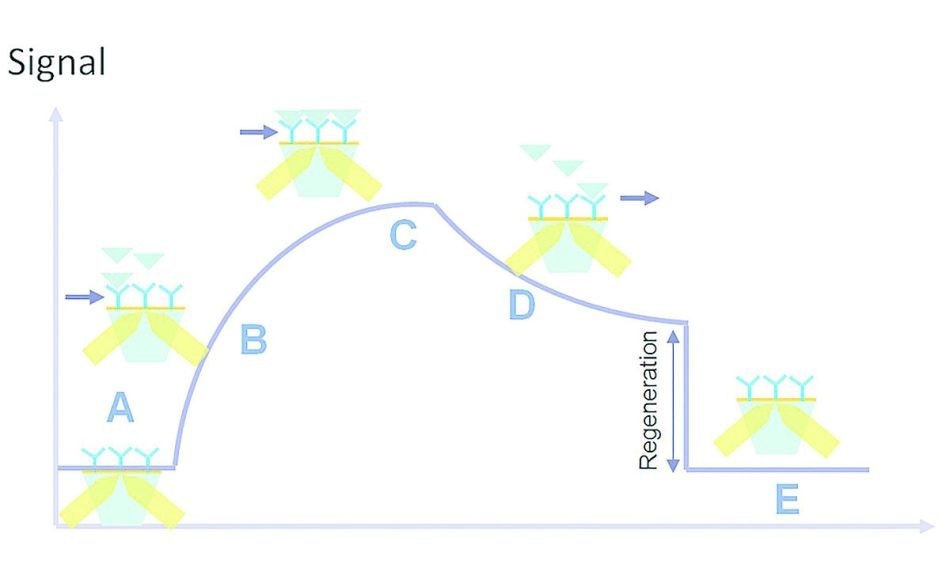
Figure 3. Kinetic interaction curve: (A) latency time, (B) association, (C) saturation, (D) dissociation, (E) regeneration.
Once the sample solution is injected, it is necessary for the analyte to enter the flow cell so that the analyte-ligand interaction can occur. There is a brief gap called the latency time (A) between the injection of the sample solution and the entry of the analyte into the flow cell. This is followed by the association phase (B) in which analyte entry and interaction with the surface ligands occur.
This ends in the plateau phase (C) which is due to the status of the molecule, such as equilibrium, consumption of the injected volume or saturation. Cessation of analyte flow is followed by the dissociation phase (D). Buffer is run through the flow cell, leading to analyte dissociation from the immobilized ligands.
In some interactions, the affinity is too high for the analyte-ligand complexes to be completely dissociated in this phase. This is handled by the injection of a regeneration solution which ensures all residual analyte is removed, in a regeneration step (E). Now the flow cell is ready for a new sample solution to be injected.
How are the Affinity Values Calculated from the Kinetic Curves?
Kinetics Parameters
ka or kass is the association rate constant (M-1.s-1), while kd or kdiss is the dissociation rate constant (s-1). The affinity between molecules can be assessed by a simple model of SPR interactions derived from the SPR kinetics data. A typical model operates on the assumption of equimolar interaction between a single ligand (L) with a single analyte (A):
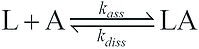
Based on this model it is possible to derive formula for kinetic curves, for both the association response (Ra) and the dissociation response (Rd). In this case, the result obtained is the reflectivity variation:
Ra(t)=Req•(1-exp[-kobs•(t-t0)]) (association)
Rd(t)=Rd(t1) • exp[-koff•(t-t1)] (dissociation)
With kobs = kass • Ci+kdiss.
- Kobs is the observed on-rate constant during the association phase of this response.
- Ci is the concentration of the injected analyte.
- koff = kdiss is the off-rate constant during the dissociation phase of this response.
- t0 and t1 are the beginning of the association and of the dissociation, respectively.
The kinetics parameters kass and kdiss are calculated by fitting the association and dissociation phases of the interaction to a mono-exponential curve, ideally with the help of the ScrubberGen or EzFit software which is Scrubber-based.
Affinity Parameters
KA is the affinity constant (M-1)
KD is the equilibrium constant (M)
Once the kinetics parameters are determined it is possible to calculate the affinity constant between two molecules as follows:
KA = 1/KD = ka/kd
Another method to calculate the affinity parameters is by using a Langmuir fit with the equilibrium values.
How are the thermodynamics coefficients determined from affinity values?
Thermodynamics Parameters
ΔG is the free energy change
ΔH is the enthalpy change
ΔS is the entropy change
ΔG can be found using the affinity constant or dissociation constant:
ΔG = R • T • ln(KD)
where R is the gas constant, T is absolute temperature (K) and KD is expressed in M.
ΔH and ΔS determination require the finding of affinity parameters at multiple temperatures, by fitting the non-linear Van’t Hoff equation to the data, and ΔG is calculated from these values.
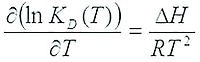
ΔG = ΔH-T•ΔS, and this enables the determination of the entropy change as well.

This information has been sourced, reviewed and adapted from materials provided by HORIBA.
For more information on this source, please visit HORIBA.