Metallic three-dimensional lattice structures harbor different mechanical properties. This article considers research published in the journal Materials, that analyzes the energy absorption properties of enhanced pyramidal lattice structures of three strut materials prepared by 3D printing, combined with investment casting and direct metal additive manufacturing.

Study: Compressive and Energy Absorption Properties of Pyramidal Lattice Structures by Various Preparation Methods. Image Credit: Iaremenko Sergii/Shutterstock.com
Cellular materials are vital structural and functional materials owing to their high specific strength, low density, and porous structure, etc. Traditional cellular materials were mostly sponges, foams, and honeycombs, with numerous limitations. However, recently generated three-dimensional lattice structures can combat the limitations of traditional cellular materials.
These materials are used in many engineering fields, for instance, the aerospace, aviation, and automotive industries.
Cellular materials have many important properties, one among them being energy absorption capacity, and this property can be tailored. Numerous methods are employed to tailor the energy absorption capacity.
Metallic lattice structures are manufactured with numerous methods like stamping forming, extrusion combining, wire cutting, expanded sheet folding, and investment casting. However, these techniques require bonding or welding techniques to assemble the struts to form lattice structures.
To address this, new metallic additive manufacturing technologies were developed, but these too have limitations, resulting in only a small part of metals suitable for these technologies. New technology has been developed combining 3D printing with investment casting, addressing the issues of the former methods.
This article, based on research in the journal Materials, compares pyramidal lattice structures in three strut materials developed with two preparation methods. The influence of preparation methods and design parameters on their compression response and energy absorption are analyzed by finite element analysis and compression tests.
Methodology
Preparation of Lattice Structure Samples
The study analyzes two technologies—direct 3D printing and 3D printing combined with investment casting. Both these techniques were used to prepare the lattice structure samples.
In direct 3D printing, a BLT-A300 printer and selective laser melting (SLM) method were used, while in 3D printing combined with investment casting an as-cast AlSi10Mg alloy and a 7005 aluminum alloy were used.
To analyze the mechanical properties of various aluminum alloys employed, tensile experiments were carried out. Figure 1a shows the geometric dimensions of samples employed for the tensile test, and Figure 1b depicts the stress-strain curves of related alloys.
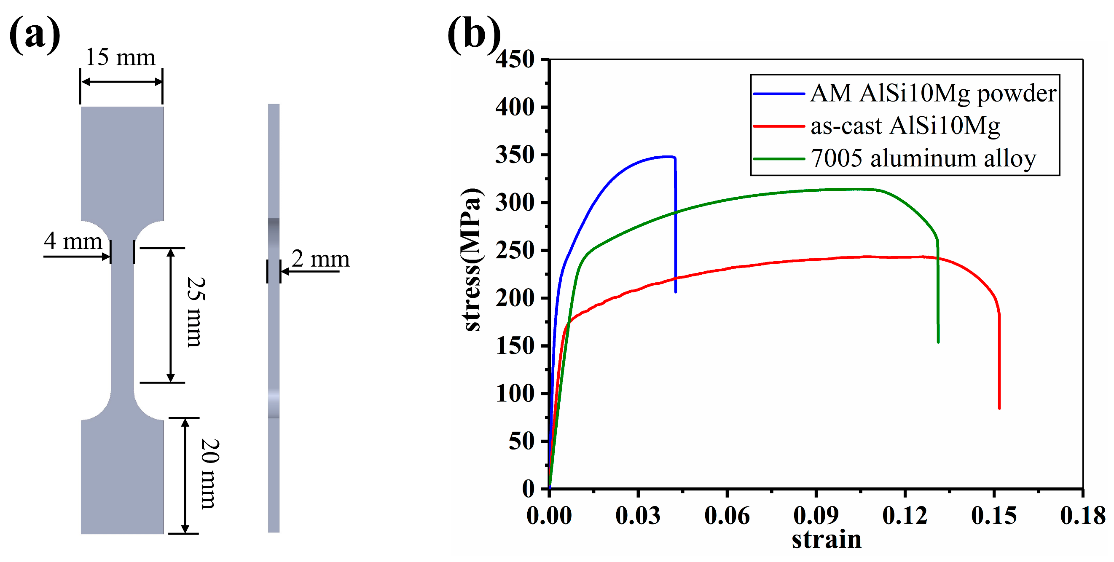
Figure 1. The tensile test of different aluminum alloys, (a) is the geometric dimensions of tensile sample; (b) is the stress-strain curves. Image Credit: Zhang, et al., 2021.
Enhanced Pyramidal Lattice Structure
The mechanical properties of the lattice structure are enhanced through node enhancement. Figure 2 shows an enhanced pyramidal (EP) lattice structure and a usual one, and the enhancement is realized slowly by increasing the diameter of struts toward the node.
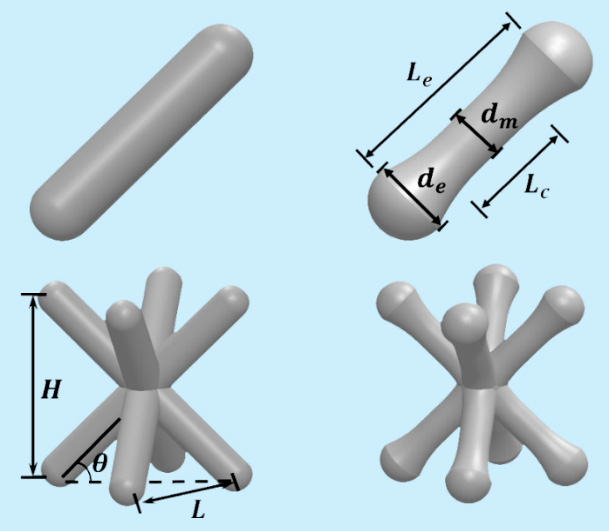
Figure 2. Characteristics of pyramidal lattice structures in the present study: the left is usual and the right is enhanced. Image Credit: Zhang, et al., 2021.
The lattice structures are grouped into four (Table 1). A1 is selected as an example (Figure 3), and at least three samples are tested for each structure. The arithmetic mean value is considered to be the representative value.
| Group |
de (mm) |
dm (mm) |
Strut Material |
θ(°) |
H (mm) |
ρ* |
| A1 |
1.70 |
1.25 |
AlSi10Mg powder |
35 |
5.00 |
0.3278 |
| A2 |
1.70 |
1.25 |
as-cast AlSi10Mg |
35 |
5.00 |
0.3278 |
| A3 |
1.70 |
1.25 |
as-cast 7005 |
35 |
5.00 |
0.3278 |
| B1 |
1.70 |
1.25 |
AlSi10Mg powder |
45 |
6.16 |
0.3486 |
| B2 |
1.70 |
1.25 |
as-cast AlSi10Mg |
45 |
6.16 |
0.3486 |
| B3 |
1.70 |
1.25 |
as-cast 7005 |
45 |
6.16 |
0.3486 |
| C1 |
1.70 |
1.25 |
AlSi10Mg powder |
55 |
7.14 |
0.3938 |
| C2 |
1.70 |
1.25 |
as-cast AlSi10Mg |
55 |
7.14 |
0.3938 |
| C3 |
1.70 |
1.25 |
as-cast 7005 |
55 |
7.14 |
0.3938 |
| D1 |
1.40 |
1.40 |
AlSi10Mg powder |
35 |
5.00 |
0.3307 |
| D2 |
1.50 |
1.34 |
AlSi10Mg powder |
35 |
5.00 |
0.3415 |
| D3 |
1.60 |
1.31 |
AlSi10Mg powder |
35 |
5.00 |
0.3484 |
| D4 |
1.70 |
1.25 |
AlSi10Mg powder |
35 |
5.00 |
0.3278 |
| D5 |
1.80 |
1.18 |
AlSi10Mg powder |
35 |
5.00 |
0.3410 |
Table 1. Parameters of lattice structures. Source: Zhang, et al., 2021.
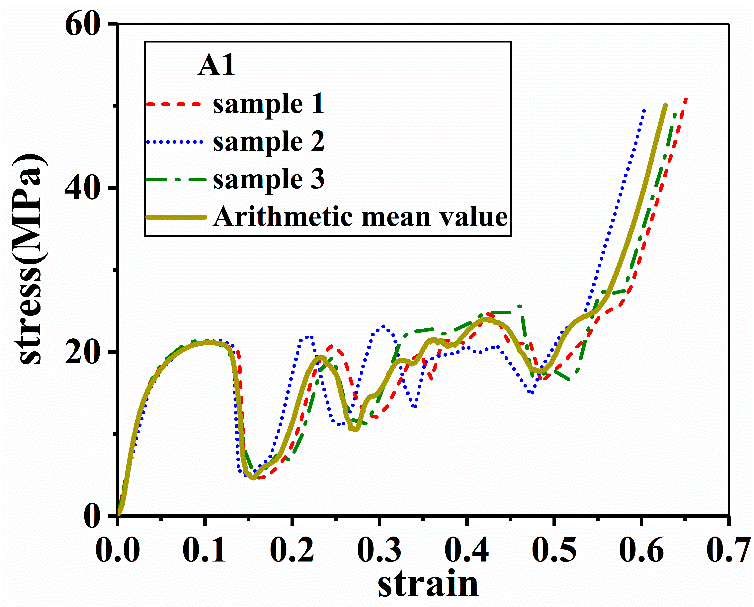
Figure 3. Arithmetic mean value of three experimental data. Image Credit: Zhang, et al., 2021.
Finite Element Analysis
The finite element analysis (FEA) was carried out to simulate the mechanical response of lattice structures in compression. Table 2 shows relevant plastic parameters.
| AlSi10Mg Powder |
As-Cast AlSi10Mg |
7005 Aluminum Alloy |
| Plastic Strain |
Stress (MPa) |
Plastic Strain |
Stress (MPa) |
Plastic Strain |
Stress (MPa) |
| 0 |
116.94 |
0 |
113.91 |
0 |
119.03 |
| 0.0037 |
218.19 |
0.0126 |
149.27 |
0.0106 |
236.02 |
| 0.0077 |
255.68 |
0.0262 |
177.05 |
0.0210 |
262.08 |
| 0.0116 |
283.78 |
0.0396 |
187.70 |
0.0316 |
277.13 |
| 0.0156 |
307.31 |
0.0529 |
201.83 |
0.0421 |
289.14 |
| 0.0195 |
325.19 |
0.0661 |
211.70 |
0.0527 |
298.12 |
| 0.0234 |
338.82 |
0.0769 |
220.06 |
0.0632 |
304.61 |
| 0.0268 |
347.14 |
0.0919 |
227.16 |
0.0738 |
309.03 |
| 0.0334 |
357.75 |
0.1194 |
234.41 |
0.0843 |
311.99 |
| 0.0398 |
362.30 |
0.1345 |
243.31 |
0.0998 |
313.59 |
Table 2. Plastic parameters of three strut materials. Source: Zhang, et al., 2021.
Compression Tests
Uniaxial compression tests were performed in a material testing system. The samples had 5 × 5 × 5 unit cells (Figure 4) to decrease the size effect. The deformation mechanism of samples was recorded by a high-resolution digital camera.

Figure 4. Four group samples, A, B, C, and D, of node-enhanced pyramidal lattice structures. Image Credit: Zhang, et al., 2021.
Results and Discussion
Compression Behaviors of Samples
Figure 5 provides the deformation mechanisms of samples in Group A, B, and C, where three various included angles and matrix material states were analyzed.

Figure 5. Deformation process of EP lattice structures in Group A, B, and C; (a–c) represent the compression when the included angle is 35°, 45°, and 55°, respectively. Image Credit: Zhang, et al., 2021.
Figure 6 and Figure 7 depict the results of FEA and the corresponding stress-strain curves.
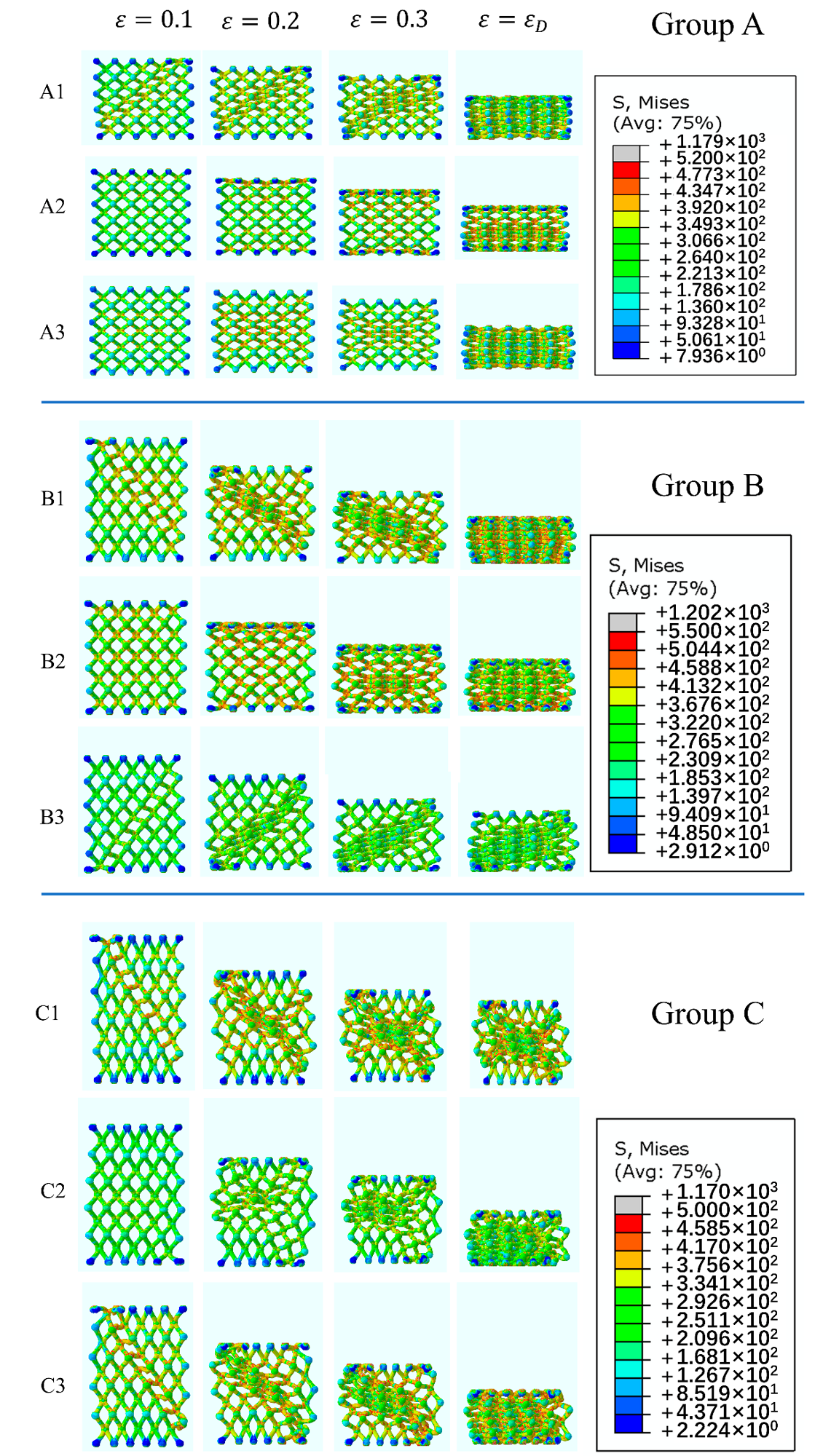
Figure 6. Mises stress distribution diagrams of EP lattice structures in Group A, B, and C. Image Credit: Zhang, et al., 2021.
Figure 7 shows that in all situations, only as-cast AlSi10Mg alloy displayed smooth stress-strain curves.
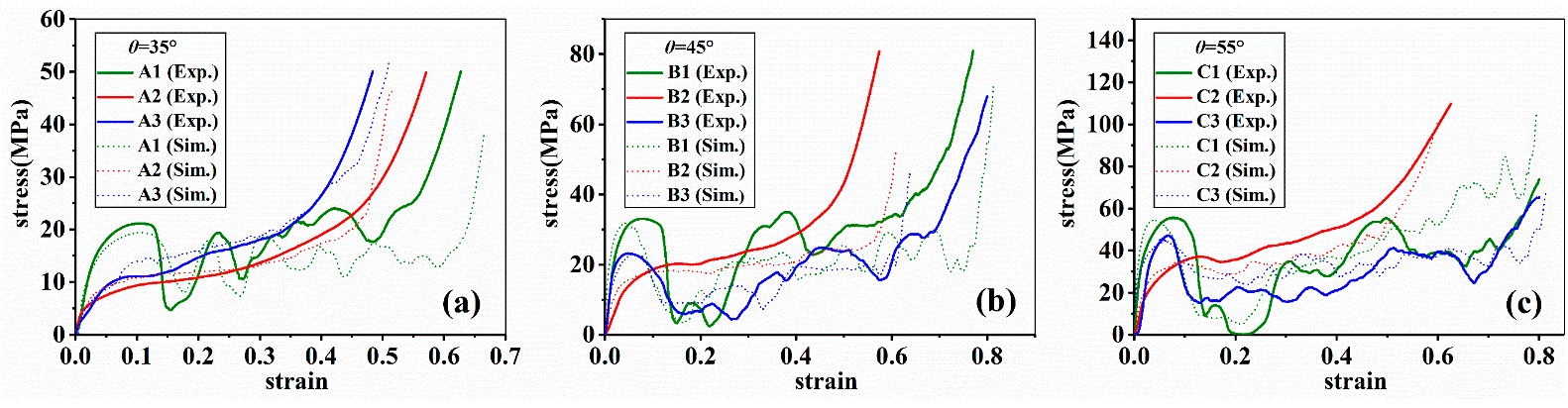
Figure 7. The stress-strain curves of samples; (a–c) represent Group A, B, and C respectively. Image Credit: Zhang, et al., 2021.
The observations show that the mechanical properties of the strut material can be the decisive factor for the response behavior of related lattice structures, and are verified by the failure mechanisms depicted in Figure 8.
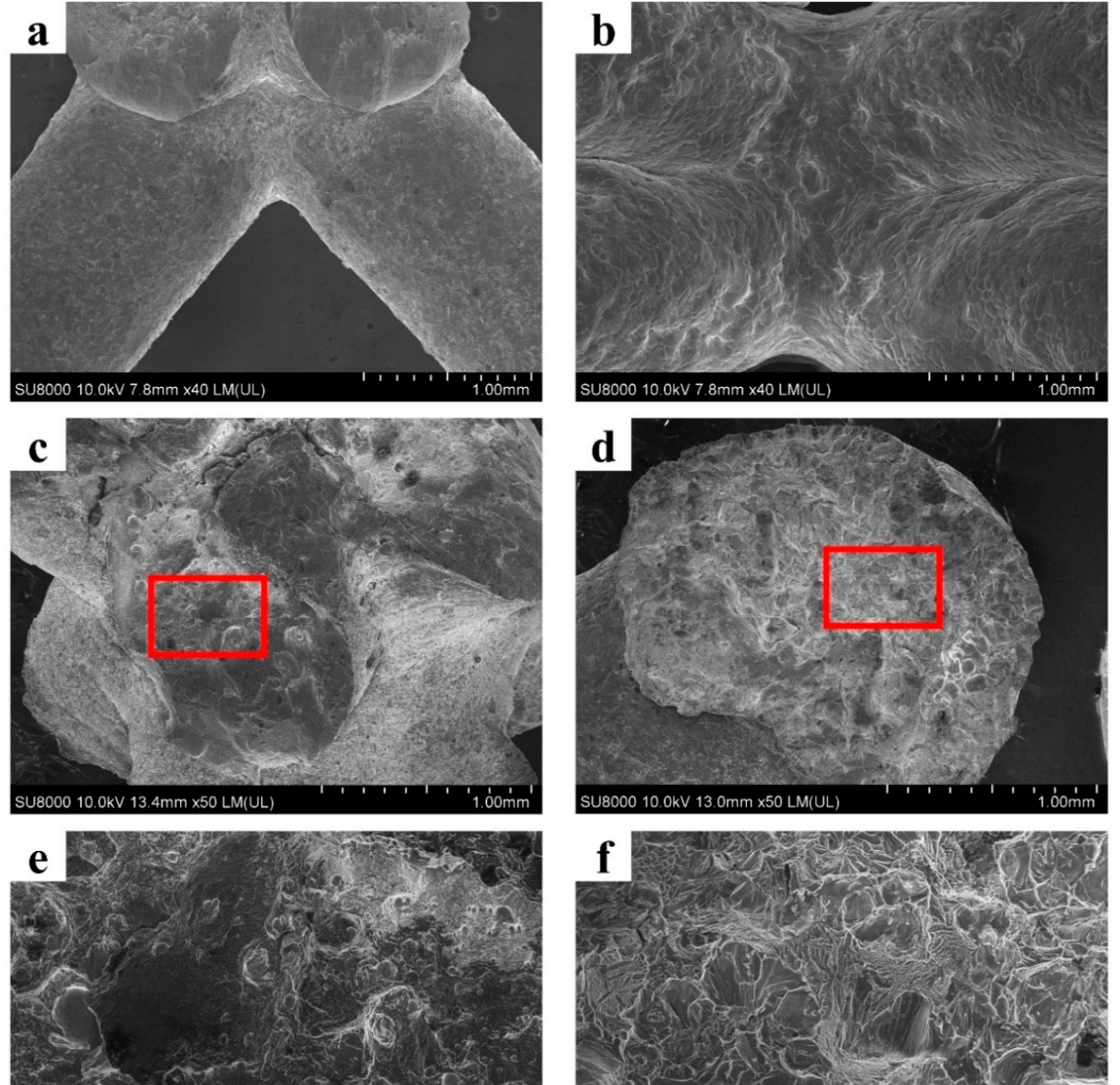
Figure 8. The strut surface morphology of (a) AM AlSi10Mg and (b) as-cast 7005 Al alloy lattice structures; (c,d) are the morphology of fracture surface of AM AlSi10Mg and as-cast 7005 Al alloy lattice structures; (e,f) magnified microstructures in the red frames of (c,d). Image Credit: Zhang, et al., 2021.
Figure 9a illustrates the compression deformation mechanism of usual and enhanced lattice structures while Figure 9b depicts the corresponding Mises stress distribution diagrams.
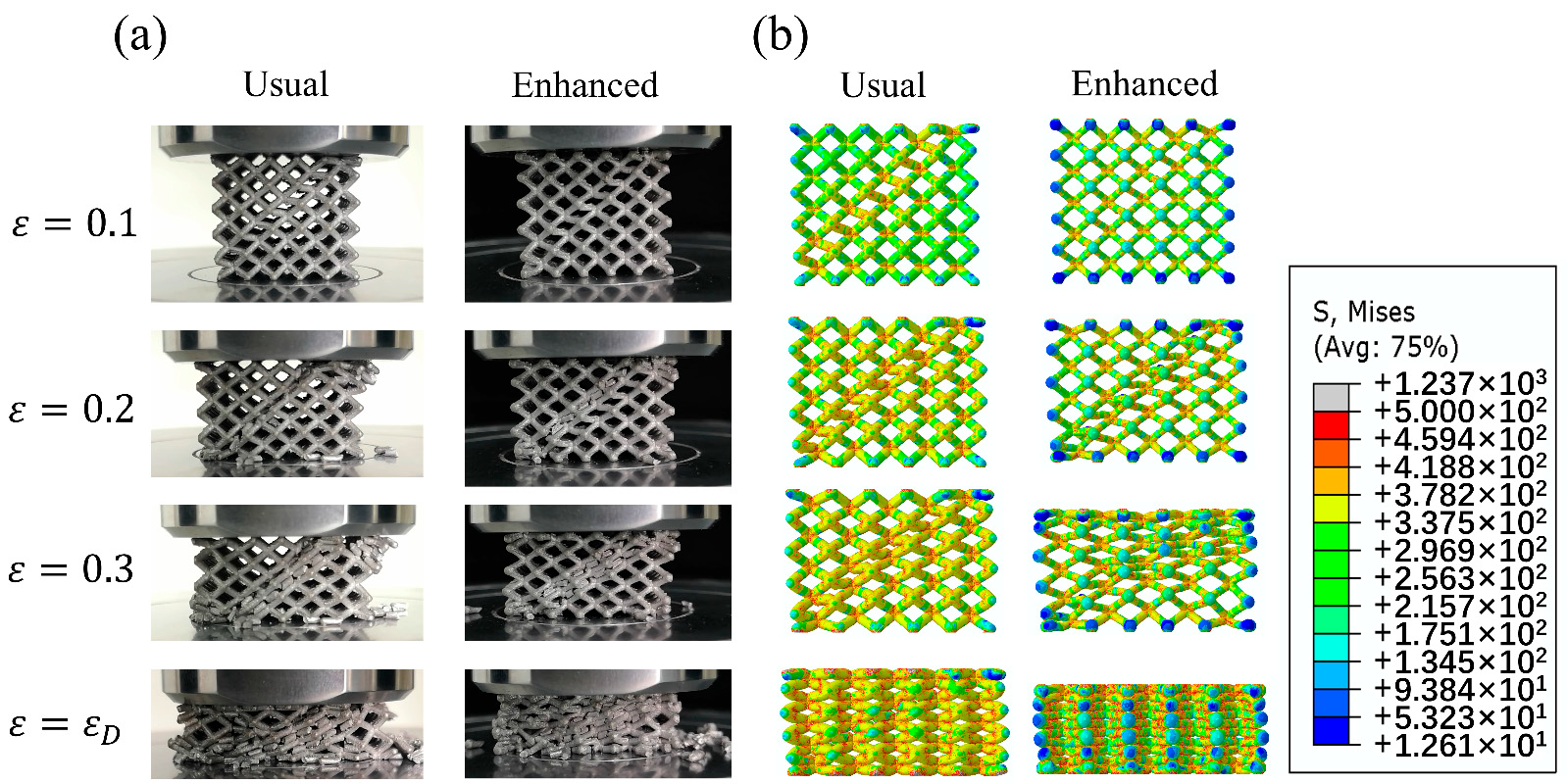
Figure 9. Deformation process of usual lattice structure D1 and EP sample D4 (a) and corresponded Mises stress distribution (b). Image Credit: Zhang, et al., 2021.
Figure 10 shows that the improved structures largely decreased stress concentration in comparison to the usual pyramidal lattice structure.
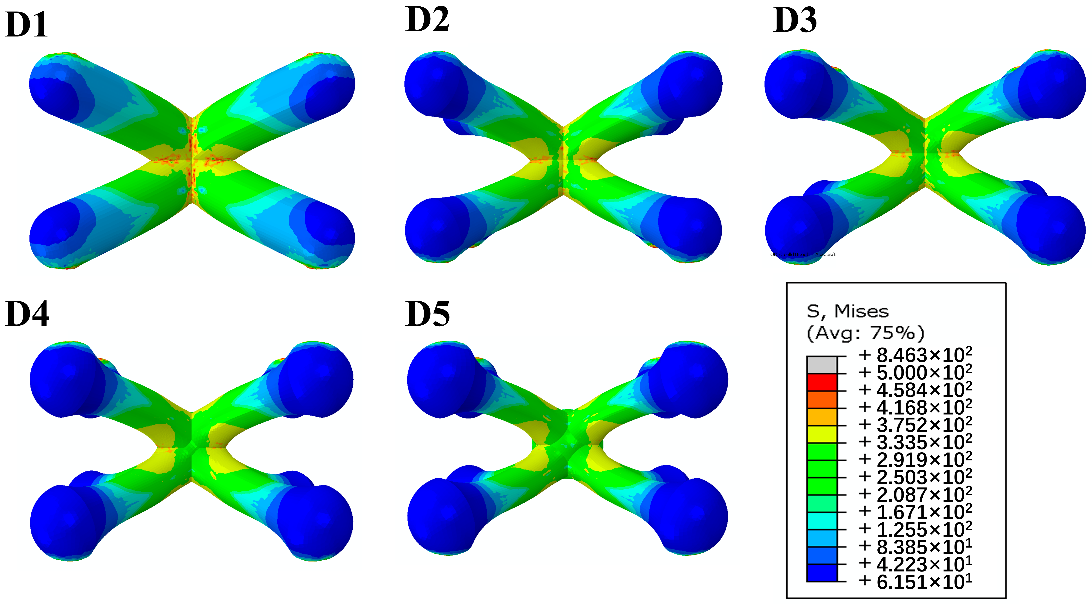
Figure 10. Mises stress distribution diagrams of a unit cell with different end diameters. Image Credit: Zhang, et al., 2021.
The compressive stress-strain curves of samples at end diameters of struts are depicted in Figure 11.
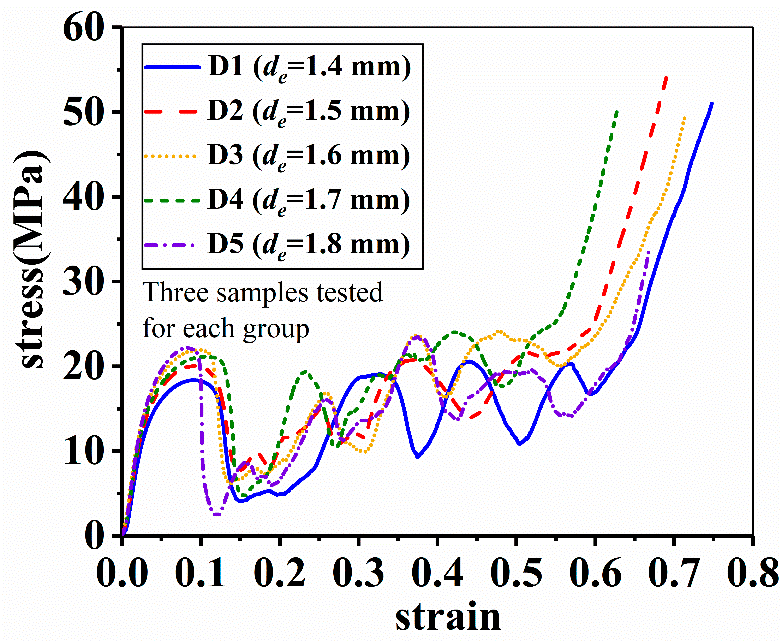
Figure 11. Effect of end diameter on the compressive stress-strain behavior of samples. Image Credit: Zhang, et al., 2021.
Energy Absorption
Table 3 shows the representation of mechanical properties derived from experimental and simulated results.
| Sample |
σP (MPa)
Exp./Sim. |
E* (MPa)
Exp./Sim. |
WVmax (mJ.mm-3)
Exp./Sim. |
Pmax (%)
Exp./Sim. |
| A1 |
21.93/19.43 |
601.46/591.11 |
10.13/8.54 |
42.45/43.95 |
| A2 |
9.55/10.89 |
185.49/197.56 |
5.60/5.07 |
24.46/28.21 |
| A3 |
11.02/13.67 |
169.27/192.00 |
4.58/5.27 |
22.26/23.79 |
| B1 |
33.05/31.94 |
1205.86/1432.18 |
15.04/14.42 |
42.98/45.16 |
| B2 |
20.18/18.03 |
346.52/426.81 |
8.69/10.99 |
28.18/37.41 |
| B3 |
23.07/22.99 |
931.93/940.00 |
9.59/8.79 |
40.23/38.23 |
| C1 |
55.38/54.11 |
2662.91/2842.14 |
26.64/30.38 |
47.03/37.44 |
| C2 |
37.00/34.53 |
925.26/1066.32 |
18.77/16.70 |
31.49/34.12 |
| C3 |
47.12/44.33 |
1836.72/1670.97 |
20.38/23.35 |
43.24/51.75 |
| D1 |
18.37/15.77 |
406.09/451.22 |
8.72/7.12 |
41.78/45.15 |
| D2 |
20.06/16.27 |
535.66/604.17 |
8.81/6.98 |
40.23/42.90 |
| D3 |
22.16/19.05 |
550.17/567.75 |
9.43/8.77 |
37.95/46.04 |
| D4 |
21.93/22.43 |
601.46/591.11 |
10.13/8.54 |
42.45/43.95 |
| D5 |
22.20/24.09 |
591.26/701.64 |
9.35/8.74 |
40.97/36.28 |
Table 3. Representing mechanical properties of samples. Source: Zhang, et al., 2021.
Figure 12 illustrates the absorbed energy per unit volume against the strain of all samples. The results indicate that different strut materials and different inclination angles lead to various energy absorption behaviors.
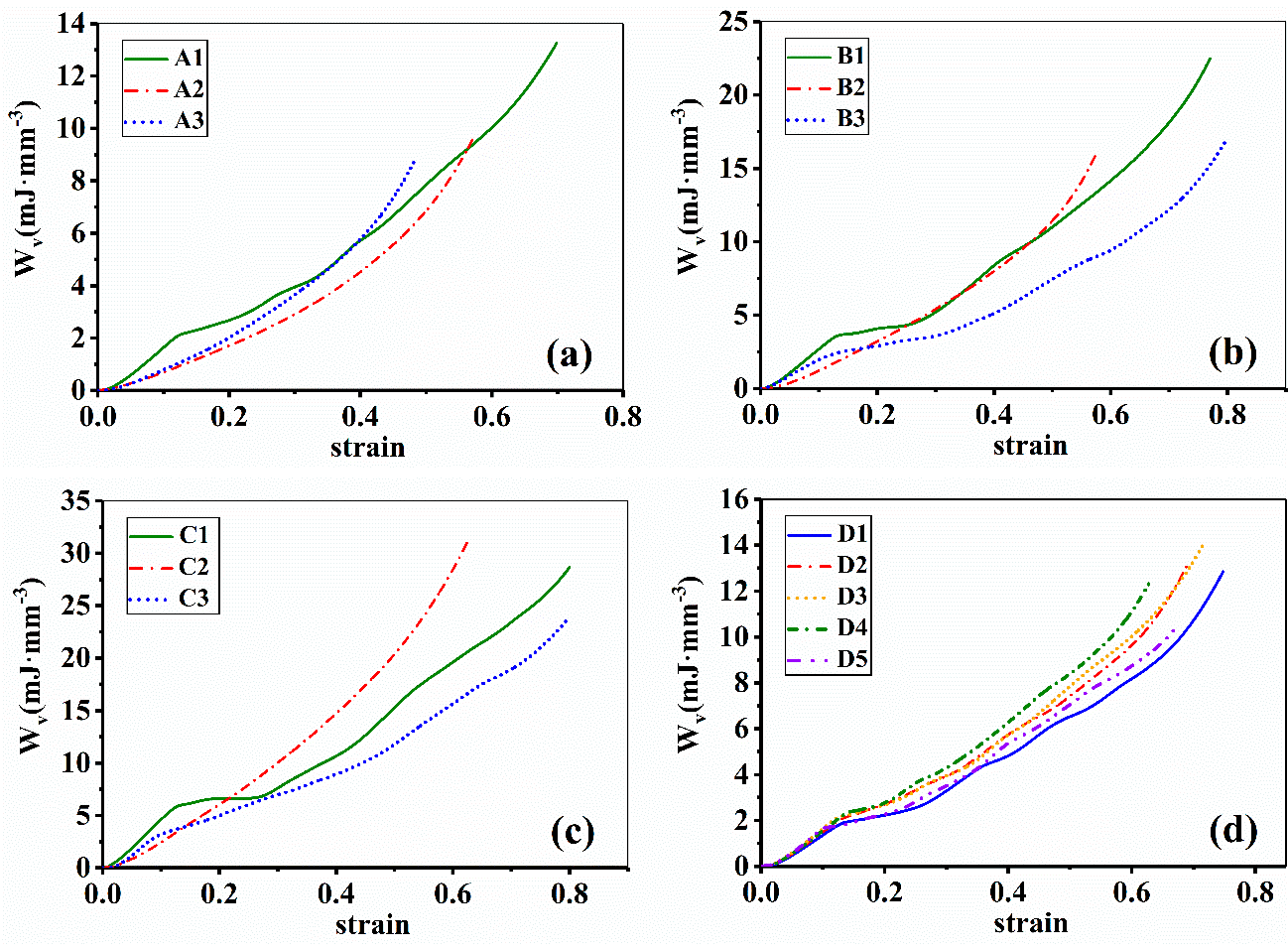
Figure 12. Absorbed energy per unit volume of EP lattice structure samples; (a–d) represents Group A–D, respectively. Image Credit: Zhang, et al., 2021.
To compare the energy absorption behavior among the three strut materials, the energy absorption diagrams were established (Figure 13a–d).
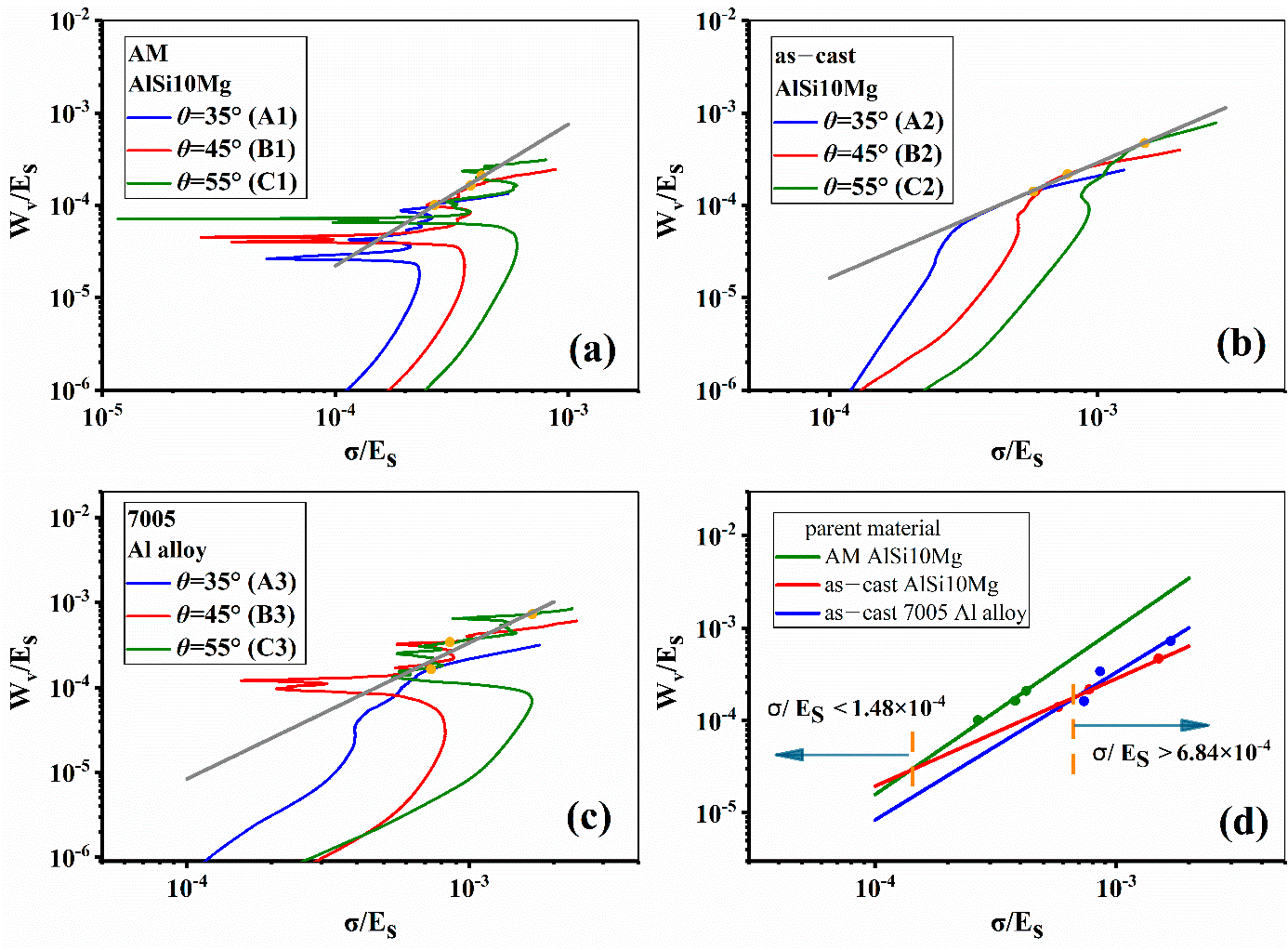
Figure 13. Energy absorption diagrams of samples with different strut materials and inclination angles; (a–c) represent the results of AM AlSi10Mg, as–cast AlSi10Mg, and 7005 Al alloy, respectively; (d) is the summary of the above results. Image Credit: Zhang, et al., 2021.
Prediction of Mechanical Parameters
Calculation of σP and E∗
The relationship between the compressive strength and relative density of foams proposed by Gibson and Ashby was applicable for lattice structures, but those did not involve the change of inclination angle of multi-layer lattice structures. Hence, another model is proposed by including the effect of inclination angle on the compressive strength of lattice structures.
Validation of Theoretical Results
Figure 14 provides the experimental and calculated results. The results show that all the fitted trajectories of mechanical parameters are straight lines, being consistent with the theoretical predictions. K and R, the constants in Table 4, showcase certain discrepancies when the strut material changes.
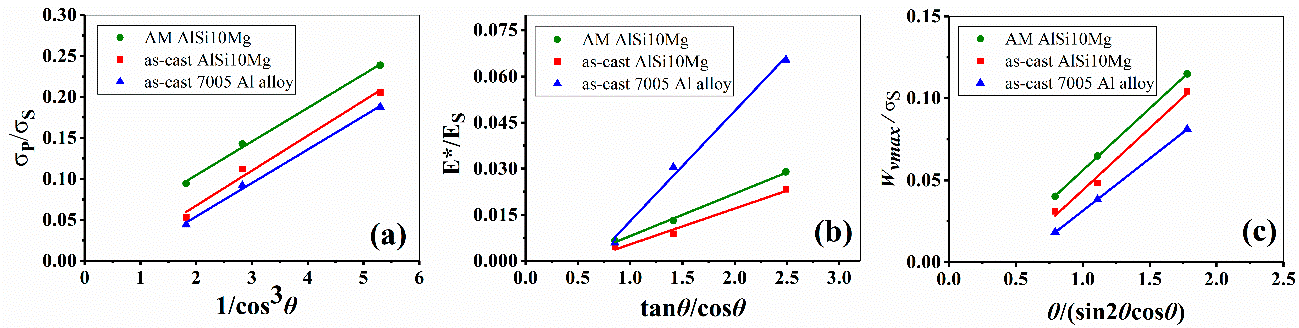
Figure 14. Theoretical results of mechanical properties against inclination angle; (a–c) are the theoretical relationship of angle with respect to compressive strength, equivalent modulus, and energy absorption, respectively. Image Credit: Zhang, et al., 2021.

Table 4. Mathematical expressions of fitted trajectories. Source: Zhang, et al., 2021.
Conclusion
The enhanced lattice structures in three strut materials were created by two preparation methods. The influence of preparing methods, strut materials, and geometric parameters on compression behavior and energy absorption was analyzed by finite element analysis and compression experiments.
It was seen that the method of 3D printing combined with investment casting removes stress fluctuations, but the compressive strength decreases. The inclination angle increase of enhanced pyramidal lattice structures channels the gap in the load-bearing capacity and enhances energy absorption. The theoretical equations and finite element analysis carried out were persistent with the experimental results.
Journal Reference:
Zhang, H., Wang, X., Shi, Z., Xue, J., Han, F. (2021) Compressive and Energy Absorption Properties of Pyramidal Lattice Structures by Various Preparation Methods. Materials. Available at: https://www.mdpi.com/1996-1944/14/21/6484/htm.
References and Further Reading
- Gibson, L J & Ashby, M F (1997) Cellular Solids: Structure and Properties. Cambridge University Press: Cambridge, UK. doi.org/10.1557/mrs2003.79.
- Lu, G & Yu, T (2003) Energy Absorption of Structures and Materials. Woodhead Publishing Ltd.: Cambridge, UK.
- Papka, S D & Kyriakides, S (1994) In-plane compressive response and crushing of honeycomb. Journal of the Mechanics and Physics of Solids, 42, pp. 1499–1532. doi.org/10.1016/0022-5096(94)90085-X.
- Zhang, X & Zhang, H (2013) Optimal design of functionally graded foam material under impact loading. International Journal of Mechanical Sciences, 68, pp. 199–211. doi.org/10.1016/j.ijmecsci.2013.01.016.
- Ivanez, I., et al. (2017) Compressive deformation and energy-absorption capability of aluminium honeycomb core. Composite Structures, 174, pp. 123–133. doi.org/10.1016/j.compstruct.2017.04.056.
- Evans, A. G., et al. (2001) The topological design of multifunctional cellular metals. Progress in Materials Science, 46, pp. 309–327. doi.org/10.1016/S0079-6425(00)00016-5.
- Fleck, N. A., et al. (2010) Micro-architectured materials: Past, present and future. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 466, pp. 2495–2516. doi.org/10.1098/rspa.2010.0215.
- Deshpande, V. S., et al. (2001) Effective properties of the octet-truss lattice material. Journal of the Mechanics and Physics of Solids, 49, pp. 1747–1769. doi.org/10.1016/S0022-5096(01)00010-2.
- Yin, S., et al. (2011) Pyramidal lattice sandwich structures with hollow composite trusses. Composite Structures, 93, pp. 3104–3111. doi.org/10.1016/j.compstruct.2011.06.025.
- Gümrük, R., et al. (2013) Static mechanical behaviours of stainless steel micro-lattice structures under different loading conditions. Materials Science and Engineering: A, 586, pp. 392–406. doi.org/10.1016/j.msea.2013.07.070.
- Tancogne-Dejean, T., et al. (2016) Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading. Acta Materialia, 116, pp. 14–28. doi.org/10.1016/j.actamat.2016.05.054.
- Ozdemir, Z., et al. (2016) Energy absorption in lattice structures in dynamics: Experiments. International Journal of Impact Engineering, 89, pp. 49–61. doi.org/10.1016/j.ijimpeng.2015.10.007.
- Gautam, R., et al. (2018) Printing and characterisation of Kagome lattice structures by fused deposition modelling. Materials & Design, 137, pp. 266–275. doi.org/10.1016/j.matdes.2017.10.022.
- Hammetter, C. I., et al. (2013) Pyramidal Lattice Structures for High Strength and Energy Absorption. Journal of Applied Mechanics, 80, p. 041015. doi.org/10.1115/1.4007865.
- Plocher, J & Panesar, A (2020) Effect of density and unit cell size grading on the stiffness and energy absorption of short fibre-reinforced functionally graded lattice structures. Additive Manufacturing, 33, p. 101171. doi.org/10.1016/j.addma.2020.101171.
- Tarlochan, F (2021) Sandwich Structures for Energy Absorption Applications: A Review. Materials, 14, p. 4731. doi.org/10.3390/ma14164731.
- Maskery, I., et al. (2016) A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting. Materials Science and Engineering: A, 670, pp. 264–274. doi.org/10.1016/j.msea.2016.06.013.
- Al-Saedi, D. S. J., et al. (2018) Mechanical properties and energy absorption capability of functionally graded F2BCC lattice fabricated by SLM. Materials & Design, 144, pp. 32–44. doi.org/10.1016/j.matdes.2018.01.059.
- Liu, H. C., et al. (2019) Flatwise compression property of hierarchical thermoplastic composite square lattice. Composite Structures, 210, pp. 118–133. doi.org/10.1016/j.compstruct.2018.11.047.
- Tancogne-Dejean, T & Mohr, D (2018) Stiffness and specific energy absorption of additively-manufactured metallic BCC metamaterials composed of tapered beams. International Journal of Mechanical Sciences, 141, pp. 101–116. doi.org/10.1016/j.ijmecsci.2018.03.027.
- Li, Z. H., et al. (2020) Mechanical properties of AlSi10Mg lattice structures fabricated by selective laser melting. Materials & Design, 192, p. 108709. doi.org/10.1016/j.matdes.2020.108709.
- Bai, L., et al. (2019) Effective Design of the Graded Strut of BCC Lattice Structure for Improving Mechanical Properties. Materials, 12, p. 2192. doi.org/10.3390/ma12132192.
- Kooistra, G. W., et al. (2004) Compressive behavior of age hardenable tetrahedral lattice truss structures made from aluminium. Acta Materialia, 52, pp. 4229–4237. doi.org/10.1016/j.actamat.2004.05.039.
- Queheillalt, D. T., et al. (2008) Mechanical properties of an extruded pyramidal lattice truss sandwich structure. Scripta Materialia, 58, pp. 76–79. doi.org/10.1016/j.scriptamat.2007.08.041.
- Kooistra, G W & Wadley, H N G (2007) Lattice truss structures from expanded metal sheet. Materials & Design, 28, pp. 507–514. doi.org/10.1016/j.matdes.2005.08.013.
- Deshpande, V. S., et al. (2001) Foam topology bending versus stretching dominated architectures. Acta Materialia, 49, pp. 1035–1040. doi.org/10.1016/S1359-6454(00)00379-7.
- Takano, N., et al. (2017) Stochastic prediction of apparent compressive stiffness of selective laser sintered lattice structure with geometrical imperfection and uncertainty in material property. International Journal of Mechanical Sciences, 134, pp. 347–356. doi.org/10.1016/j.ijmecsci.2017.08.060.
- Maconachie, T., et al. (2019) SLM lattice structures: Properties, performance, applications and challenges. Materials & Design, 183, p. 108137. doi.org/10.1016/j.matdes.2019.108137.
- Huang, Y., et al. (2021) Compressive Behaviour of Aluminium Pyramidal Lattice Material-Filled Tubes. Materials, 14, p. 3817. doi.org/10.3390/ma14143817.
- Xue, Y. Y., et al. (2018) Compressive property of Al-based auxetic lattice structures fabricated by 3-D printing combined with investment casting. Materials Science and Engineering: A, 722, pp. 255–262. doi.org/10.1016/j.msea.2018.02.105.
- Thijs, L., et al. (2010) A study of the micro structural evolution during selective laser melting of Ti-6Al-4V. Acta Materialia, 58, pp. 3303–3312. doi.org/10.1016/j.actamat.2010.02.004.
- Miltz, J & Gruenbaume, G (1981) Evaluation of cushioning properties of plastic foams from compressive measurements. Polymer Engineering and Science, 21, pp. 1010–1013. doi.org/10.1002/pen.760211505.
- Wang, H., et al. (2019) Effect of structure design on compressive properties and energy absorption behavior of ordered porous aluminum prepared by rapid casting. Materials & Design, 167, p.107631. doi.org/10.1016/j.matdes.2019.107631.
- Maiti, S. K., et al. (1984) Deformation and energy-absorption diagrams for cellular solids. Acta Metallurgica, 32, pp. 1963–1975. doi.org/10.1016/0001-6160(84)90177-9.
- Yan, C. Z., et al. (2015) Microstructure and mechanical properties of aluminium alloy cellular lattice structures manufactured by direct metal laser sintering. Materials Science and Engineering: A, 628, pp. 238–246. doi.org/10.1016/j.msea.2015.01.063.
- Crupi, V., et al. (2017) Static behavior of lattice structures produced via direct metal laser sintering technology. Materials & Design, 135, pp. 246–256. doi.org/10.1016/j.matdes.2017.09.003.
- Zhao, M., et al. (2020) Mechanical and energy absorption characteristics of additively manufactured functionally graded sheet lattice structures with minimal surfaces. International Journal of Mechanical Sciences, 167, pp. 105262. doi.org/10.1016/j.ijmecsci.2019.105262.
- Zhang, H. R., et al. (2021) Energy absorption diagram characteristic of metallic self-supporting 3D lattices fabricated by additive manufacturing and design method of energy absorption structure. International Journal of Solids and Structures, 226–227, p. 111082. doi.org/10.1016/j.ijsolstr.2021.111082.