Dec 24 2014
The elastodynamic equations for inhomogeneous media are crucial to the seismology, the NDT of composites, the elastic metamaterials, etc. Recently, Dr. XIANG Zhihai from the Applied Mechanics Laboratory, Department of Engineering Mechanics, Tsinghua University found out that the accurate elastodynamic equations for inhomogeneous media should incorporate the gradient of pre-stresses.
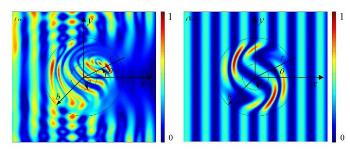These are snapshots of the normalized total displacement of plane elastic wave at 80 kHz pass through wave rotators (54°): (a) Based on the traditional equations; (b) based on the new equations. Credit ©Science China Press
This work, entitled "The form-invariance of wave equations without requiring a priori relations between field variables", has been published in SCIENCE CHINA Physics, Mechanics & Astronomy, 2014, 57(12).
It is well-known that a mirage in nature is induced by the bending of light through nonuniformly distributed refraction indices in the sky. Inspired from this natural phenomenon, many man-made inhomogeneous materials have been invented to steer the light or sound along desired trajectories to achieve meta-devices such as the cloak, the flat lens, etc. These kinds of materials are conventionally called the metamaterials. To design the metamaterial that can bend the wave coming from all directions, we can use coordinate transformation methods to obtain the effective material parameters. The basis of these transformation methods is the form-invariance of wave equations under arbitrary coordinate transformation. With the assumption that there are certain relations between field variables before and after the coordinate transformation, it has been proved that the electromagnetic and sound wave equations are form-invariant but the traditional elastodynamic equations do not have this property. In addition, although the elastodynamic equations established by Professor Willis are form-invariant, they are not widely implemented due to their abstract formulations. All these reasons stunt the development of elastic metamaterials.
This study gives general proofs of form-invariance of electromagnetic, sound and elastic wave equations without using any assumption of the relation between field variables. Thus, it reveals the form-invariance is an intrinsic property of all correct wave equations. As a by-product, new elastodynamic equations that are locally accurate to describe the elastic wave propagation in inhomogeneous media are naturally obtained. In contrast to the traditional elastodynamic equations, these new equations are very similar to the Willis equations and have additional terms that are related with the gradient of pre-stresses. Based on these new equations, a perfect elastic wave rotator and a nearly perfect elastic wave cloak have been designed.
These findings are important for solving inverse scattering problems that involve the propagation of low frequency elastic waves in inhomogeneous media, such as the seismology, the NDT of composites and the elastic metamaterials, etc.