May 23 2018
A unique form of phase change occurs in liquid crystals. At a specific temperature, their cigar-shaped molecules change from a disordered jumble to a highly ordered arrangement in which all the molecules point almost in the same direction.
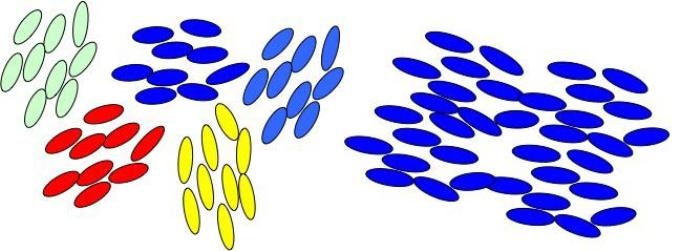Semi-ordered to ordered: Molecules in liquid crystals go from a disordered jumble to more ordered alignment with changes in temperature. But there’s evidence of an intermediate state (left) where order starts to emerge in discrete patches before arriving at the fully ordered state (right). New research by Brown University chemists helps to identify and understand that intermediate state. (Image credit: Stratt lab/Brown University)
In LCD televisions, this phase change is exploited to project distinctive colors in moving images. However, for many years, experiments have suggested the existence of another liquid crystal state, which is an intermediate state between the disordered and ordered states in which order starts to appear in discrete patches when a system reaches its transition temperature. At present, chemists from Brown University have exhibited a theoretical model for the detection of the intermediate state and for gaining better insights into the way it works.
People understand the ordered and disordered behaviors very well, but the state where this transition is just about to happen isn’t well understood. What we’ve come up with is a sort of yardstick to measure whether a system is in this state. It gives us an idea of what to look for in molecular terms to see if the state is present.
Richard Stratt, Co-Author & Professor of Chemistry at Brown
The study, which has been reported in the Journal of Chemical Physics, could provide valuable insights into liquid crystals and also molecular motion elsewhere in nature - for instance, phenomena such as the protein tangles attributive to Alzheimer’s disease. The study was headed by Yan Zhao, a PhD student in Stratt’s lab who expects to graduate from Brown this spring.
To perform the research, the scientists adopted computer simulations of phase changes in a simplified liquid crystal system with a few hundred molecules. The simulation results were analyzed by using random matrix theory, a statistical model usually used for describing chaotic or complex systems. The researchers demonstrated that although the theory proved favorable in describing the system in the ordered as well as the disordered states, it failed to describe the transition state. This discrepancy from the theory can be adopted as a probe for identifying the regions of the material in which order starts to appear.
“Once you realize that you have this state where the theory doesn’t work, you can dig in and ask what went wrong,” stated Stratt. “That gives us a better idea of what these molecules are doing.”
According to random matrix theory, it is predicted that the sums of uncorrelated variables - here, the directions in which molecules point - should form a bell curve distribution upon being plotted on a graph. Stratt and Zhao demonstrated that this holds true in the case of the molecules in liquid crystals when they are in the disordered and ordered states. In the disordered state, the bell curve distribution is formed by the completely random orientations of the molecules. In the ordered state, although the molecules are lined up along a common axis, each of them deviates from it a little. Some of them point a little to the left of the axis and some a little to the right. It is possible to fit such random deviations, similar to the random molecule positions in the disordered state, to a bell curve.
However, the bell curve distribution falls apart just before the phase change occurs, as the temperature of the system decreased to its transition temperature. This indicates that molecules in discrete patches in the system became associated with one another.
You now have several sets of molecules starting to cooperate with each other, and that causes the deviations from the bell curve. It’s as if these molecules are anticipating that this fully ordered state is going to take place, but they haven’t all decided which direction they’re going to face yet. It’s a little like politics, where everybody agrees that something needs to change, but they haven’t figured out exactly what to do.
Richard Stratt, Co-Author & Professor of Chemistry at Brown
According to Stratt, this study could provide better insights into the phenomenon which regulates the effectiveness of molecular motion. Molecules are relatively free to move in both ordered and disordered liquid crystals. However, in the intermediate state, that movement becomes restricted. Then, this state depicts a condition in which the molecular advancement starts becoming gradual.
There are a lot of problems in natural science where movement of molecules is slow. The molecules in molten glass, for example, progressively slow down as the liquid cools. The protein tangles involved in Alzheimer’s disease are another example where the molecular arrangement causes the motion to be slow. But what rules are governing those molecules as they slow down? We don’t fully understand it.
Richard Stratt, Co-Author & Professor of Chemistry at Brown
Stratt believes that an in-depth knowledge of slow molecular movement in liquid crystals could provide a blueprint for perceiving slow movement elsewhere in nature.
The National Science Foundation (CHE-1565540) supported this study.