Scientists Test Stress Properties of Flexible Phone Screens

By Surbhi JainReviewed by Susha Cheriyedath, M.Sc.Apr 18 2022

In an article recently published in the open-access journal Materials, researchers presented an analysis of the mechanical characteristics of flexible screens.

Study: Analysis on the Mechanical Behavior of Flexible Screens. Image Credit: racksuz/Shutterstock.com

Background

Flexible organic light-emitting devices (OLEDs) have become increasingly essential in smart clothing, flexible displays, and other industries in recent years. The structural stability and optimization of the flexible OLED screens have become significant criteria to address the considerations of portability and economics as OLEDs become more widely used in display goods.

The narrow bending radius leads the gadget to be overstressed during the bending operation, causing it to rip off and inflict irreparable damage to the screen. The finite element method can be used to identify the mechanism of damage and peeling of the adhesive layer of the flexible OLED screen, which can obtain stress and strain results.

Using a new technology (ball milling process) and green halogen-free solvent, a novel hole-transport layer for the host material was produced, which not only enhanced the photoelectric response of the optical monomer-based thin-film device, but also exhibited good stability under continuous stress. However, there is a gap between the stacking structure and the actual flexible screen module.

Geometric structure model of U-shaped bending mode. The left reference point was fixed, and the bending was performed by moving the fixture board from position A to position B within the bending time t seconds. The lateral gap was πR since the bending angle was π and the bending radius was R. Image Credit: Niu, L et al., Materials

About the Study

In this study, the authors presented the bending model for the flexible screen using finite element analysis. An imaging experiment was conducted to estimate the growth of Mises stress as the bending radius decreased for common U-shaped bending and the redistribution of the tensile and compression zones. A water-drop-shaped bending mode was also investigated in order to lessen the possibility of structural collapse.

The team established the flexible screen module's real stacking model using the finite element software ABAQUS. The mechanical behavior of the OLED flexible screen, OCA thickness-shape, the impact of the bending radius, and the bending mode (including water-drop-shaped and U-shaped) were discussed. An imaging experiment was carried out to confirm the analysis' findings.

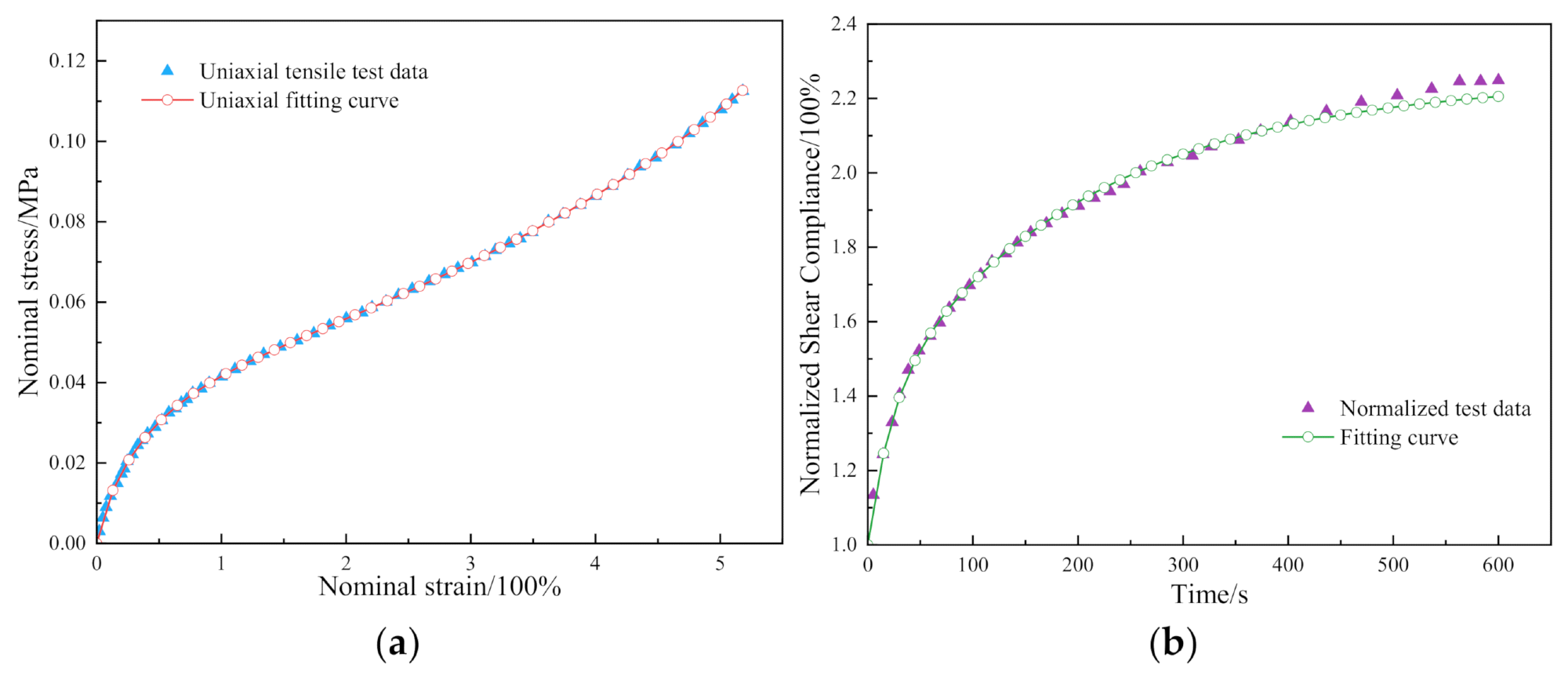
(a) The fitting result of the OCA for the Ogden model; (b) the fitting result of the OCA for the Prony model. Image Credit: Niu, L et al., Materials

The researchers simulated the flexible screen's mechanical behavior using a finite element model created using ABAQUS. A fixture board and the screen module were cemented together, and the fixture board's movement drove the screen's bending. The bending radius was set to R, the bending angle to π, the beginning lateral gap was πR, and the bending was finished in t seconds for a common U-shaped bending mode.

The multi-layered films with varying mechanical properties made up the flexible screen module. OCA bonded the film layers and coordinated the deformation of each layer during the folding process, which was important for the structure of the flexible screen module. For a 180-degree folding simulation, the bending radii were set to 3 mm, 2.5 mm, 2 mm, 1.5 mm, and 1 mm, respectively, with a bending time of t = 18 s.

Observations

According to the analysis, the bending would not only function effectively with a short bending radius, but it would also lower the danger of the structure failing. The discrepancy ratio between the experimental and simulated ranges under the same bending radius was less than 1%, which confirmed the accuracy of the finite element model and the experimental data.

The spherical droplet had a radius of 2.286 mm when the bending radius was R = 2 mm. S1/S5 had a maximum increase ratio of 13.07%, S2/S5 had a maximum increment ratio of 18.56%, and S1/S5 and S2/S5 had absolute strain increment ratios of 1.0053% and 1.0042%, respectively.

On the OLED light-emitting layer, the profiles S3, S4, and S5 had similar effects, and the highest difference ratios of S3/S5 and S4/S5 are 1.27% and 3.61%, respectively. Profiles S1 and S2, on the other hand, raised the maximum stress of the OLED layer by 13.53% and 24.04%, respectively, when compared to S5. When the bending radius was 2.5 mm, the plastic strain started on the inside of the CPI layer, in the squeezed area. The outside tension area experienced no plastic strain until the bending radius reached 2 mm. The plastic strain occurred at the outer tension area when the bending radius was 1.5 mm.

The maximum tensile stress was reduced by 23.99% for R = 2.5 mm, but the maximum compressive stress was raised by 15.82%. When R = 3 mm, the maximum compressive stress was increased by 20.22% but the tensile stress was reduced by 27.54%.

(a) Experimental schematic; (b) ranging before bending (units shown in μm); (c) ranging after bending (units shown in μm). Image Credit: Niu, L et al., Materials

Conclusions

In conclusion, this study elucidated the bending model for the flexible screen using finite element analysis. It was observed that the maximum Mises stress grows fast as the bending radius was decreased in the common U-shaped bending. The OLED and BP layer stack sequences, as well as the most harmful single layer and the profiles of the OCA layer, were optimized.

The layer material selection was based on the redistribution of the tensile and compression zones, according to the optimization. An imaging experiment was done to quantify the maximum slip distance during bending in order to validate the analysis.

Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.