An OD specification is an evaluation of the amount of light that is blocked at a certain wavelength.
It is the log of the transmittance, or:
OD = 2−log (%T)
OD values are additive (shown in Figure 1). An OD value of 8 blocking at 405 nm can be achieved by using a dichroic filter with an OD of 2.5 blocking at 405 nm with an emission filter with an OD of 5 to 6 blocking at 405 nm as shown in Figure 1 below.
Note that OD values of approximately 6 or more are highly complex to measure on a traditional spectrometer. The actual blocking can be much higher than the calculated values, as demonstrated in the right panel below.
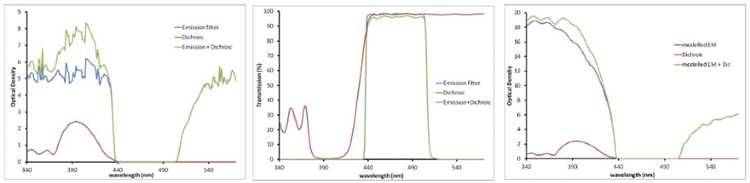
Figure 1. Emission and Dichroic filters displayed in Transmission (left) and OD (right two panels). These measurements are related by a log transformation. As %T values get very low, OD values get high. OD is an additive property (green curve on the right). The right panel shows the modeled performance of the emission filter, illustrating the much higher OD that is likely present, especially at lower wavelengths.
This article will give an example of how to determine the level of blocking necessary in a regular flow cytometer system.
Flow cytometers are designed to identify cells and particles in the range of 1 to 15 µm. Laser light scatter and fluorescence are usually used to achieve this. The samples pass through the detection system in single file, as shown in Figure 2.
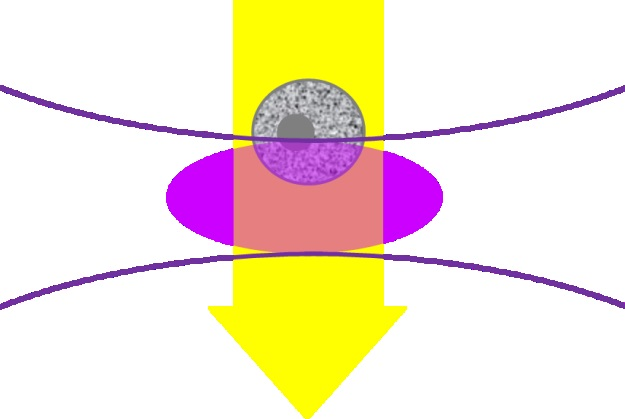
Figure 2. Illustration of the focused laser beam (lavender oval) interacting with the sample in the flow cytometer. The grey cell is moving down through the laser focus.
A commonly used flow cytometry laser is the 405 nm laser. It has a linear flow rate of 1 m/s (often seen in cell counting systems), which means any point in the cell or particle will come into contact with the illuminated volume (the lavender section presented above) for approximately 10 ms.
Using 100 mW of power, it is easy to establish the amount of photons in a sample that are interacting with a fluorophore by utilizing the equation below.
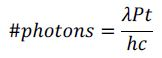
Where time (t) is in seconds, power (P) is in Watts, and wavelength (λ) is in meters. Planck’s constant (h) is 6.626x10-34 Js and the speed of light (c) is 3x108 m/s.
This article will work on the assumption that all the photons are in contact with the fluorophore for the complete duration of the analysis. The incorporation of the photon density in the remit of the focal volume of the sample would be a more thorough approach.
There are ~2*1011 photons in the focus of the beam throughout the 10 µs transit time. Some fragments of light will pass through the sample, some will be elastically scattered (Mie and Rayleigh scattering away from organelles), some will be inelastically scattered (Raman scattering), and some will be absorbed.
Misplacement of the absorbed light can occur as a result of photochemistry or heat, or can show as fluorescence, which is usually seen at a right angle to both the laser beam and the direction of the journey of the sample particles. For this example, it can be in or out of the paper’s plane.
The most complex situation would be aiming to block the laser beam and identify a single photon of fluorescence simultaneously.
For this scenario, the detection of the fluorescence signal and the blocking of 2*1011 photons at 405 nm would need to be carried out at the same time. The first suggestion would be that the emission filter needs OD 11 blocking.
This belief is not always the case. As the OD values are additive, as described earlier, adequate blocking can be achieved if the blocking values of the dichroic and emission filters add up to produce an OD value of 11, but there are more elements to consider.
In practice, a smaller amount of blocking can be used because the amount of scattered light is usually smaller compared to that of a raw laser beam. As an example, the blocking requirement will be OD9 if 1% of the light is scattered to identify one fluorescence photon in the company of this scattered signal.
In the majority of situations, it is likely to be impractical to describe the identification of a single photon. When utilizing a standard fluorescence lifetime of 10 ns for a fluorescent probe, a single fluorophore can absorb light (or be excited) 1,000 times in the 10 µs transit time.
The fluorophore’s quantum yield (Φ) describes the amount of absorbed photons that can be discerned by the system and re-emitted as fluorescence photons. It ranges from 0.2 for tryptophan to greater than 0.9 for FITC (one of the highest).
A single fluorophore using a middle value of 0.5 will produce 500 photons, translating to a blocking requirement of OD7. It is likely that every cell, protein, or particle will have a certain amount of fluorophores attached. This means the number of emitted photons will be even higher, reducing the blocking requirement even more.
If different light in the system is not well-controlled, the blocking OD should be greater. For example, uncontrolled reflections will be present in the optical system if the enclosure is not light-tight. Anti-reflection coatings can be a solution for this, as well as the use of baffles and absorbing materials.
OD is frequently over-specified which contributes to additional complexity and cost in coatings. If time is taken to consider all the photons inside of a system, the cost will be decreased and the signal will be optimized.
*A more detailed approach would entail the photon density within the sample’s focal volume.

This information has been sourced, reviewed and adapted from materials provided by Omega Optical, Inc.
For more information on this source, please visit Omega Optical, Inc.