Dynamic Light Scattering (DLS): Why are High Concentration Measurements Difficult?

Abstract

Dynamic Light Scattering (DLS) is an efficient method of measurement employed for calculating the hydrodynamic size of common nanomaterials consisting of nanoparticles, colloids, polymers and proteins. Although this method is extremely versatile, there are numerous key factors that cannot be ignored when employing light scattering to characterize high-concentration solutions.

Although it is feasible to take measurements on high volume-fraction samples without dilution, additional questions arise regarding the meaning of the hydrodynamic size. To appreciate why this is the case, two effects faced in concentrated solutions need to be discussed: multiple scattering and mutual diffusion.

Results

Equivalent Hydrodynamic Size

The size acquired from DLS is a hydrodynamic size, which comes from measurements of particle diffusion. All freely diffusing particles are continuously experiencing Brownian Motion in proportion to thermal energy stated as the product of the Boltzmann constant by the temperature (k_bT). A lone particle would experience Brownian Diffusion in inverse proportion to its size; as such, the diffusion coefficient, D_T, of this article can be employed to work out its hydrodynamic diameter, d_H, which can be seen in the Stokes-Einstein equation:

D_T = k_bT / 3πηd_H

d_H can be achieved if the temperature, T and viscosity, η, are also established. This single particle diffusion coefficient is the outcome of self-diffusion; as such, in the limit of infinite dilution, this calculated size is entirely equivalent to its hydrodynamic size. In the simplest instance, a single decay rate, Г, is extracted from the DLS autocorrelation function (ACF). This Г is the reciprocal of the characteristic relaxation time, τ_t, such that:

g⁽¹⁾(τ) = exp(-Гτ)

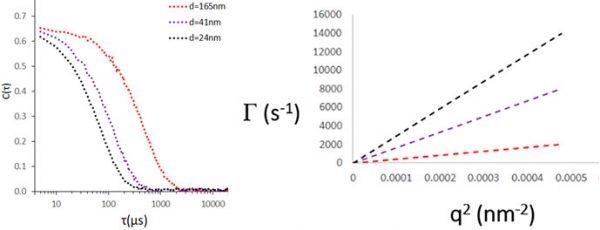
Figure 1.0. Simulated ACF’s for decay rates of Г = 7000, 4000 and 1000 s^-1 (corresponding to 24, 41 and 165 nm diameter spherical particles). The relationship between Г, and hydrodynamic size will be addressed in the following sections. Image Credit: Brookhaven Instrument Corporation

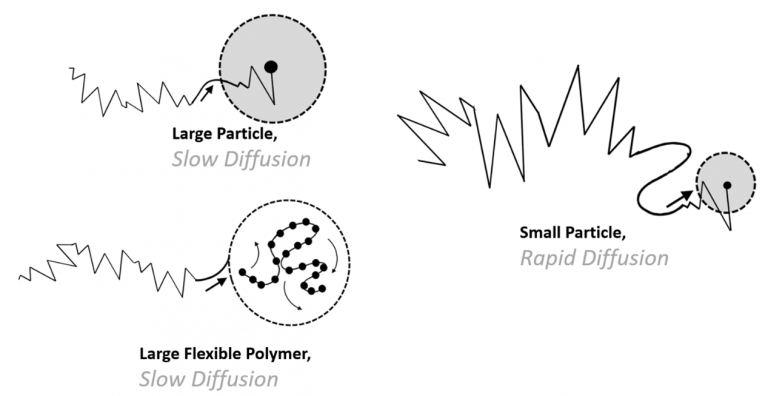
Figure 1.1. Given two spherical particles, the larger particle will diffuse more slowly. Also of note, that flexible polymers frequently have multiple modes of relaxation corresponding to diffusion and also of internal motion of the polymer chain. Image Credit: Brookhaven Instrument Corporation

The quickest decay relates to the smallest efficient particle size, which in the dilute case relates to the diffusion coefficient of a lone particle. The diffusion coefficient would arise from the slope of the above plot. However, it is very common to measure at a single q, as is true with fixed-angle DLS measurements. For most compact globular particles, a single scattering angle can be employed to achieve hydrodynamic size.

The level of diffusion of the particle directly relates to the calculated size, where fast decay rates relate to smaller particles and lower decay rates relate to larger particles. For a given q value, Г is associated with the translational diffusion coefficient, D_T, through the following expression:

D_T = Г / q²

Employing this calculation, all decays are regarded as stemming entirely from diffusion and all diffusion coefficients are regarded as though they stem from the thermal motion of a lone particle. This is frequently not the case and crucial exceptions are outlined below. This becomes increasingly complicated when interactions with other particles are measured.

Self-Diffusion vs. Mutual Diffusion

The idea of infinite dilution is an abstraction; it is not possible to measure an actual sample at a theoretical limit. By producing serial dilutions of a concentrated solution or suspension, you gradually dilute away interactions across particles. By lessening these interparticle interactions, the impact of mutual diffusion is lessened and as such, the mutual diffusion coefficient methods the value projected for self-diffusion as concentration is lessened. At extremely high concentrations, the measured diffusion coefficient would not stem from self-diffusion; as such, although it can be measured, the size calculated would not be the actual particle size. This size would not seem constant regarding concentration. Artificially less (or bigger) sizes would follow, subject to the kind of interaction.

Multiple Scattering

If the sample concentration is big enough, a lone photon of laser light will scatter off many particles successively prior to getting to the detector. The bigger the pathlength, the more secondary scattering events take place and the less correlated the discovered light is to the initial signal. In comparison to dilute solution environments, this fast loss of correlation is not the outcome of particle motion and, as such, not relevant to particle size. This can be seen in figure 1.2.

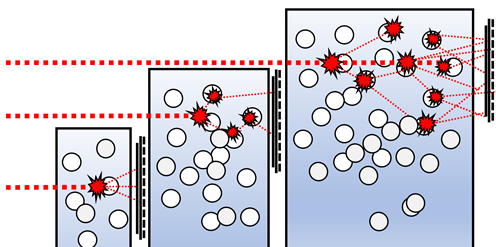
Figure 1.2. Multiple scattering is more pronounced as pathlength is increased. Image Credit: Brookhaven Instrument Corporation

As such, in the instance of multiple scattering, the signal seems to decay quicker. Consequently, this bigger decay rate would seem to be quick diffusion. In actuality, this is a non-diffusive decay; so, not only is the calculated size not a size, the diffusion coefficient it is being determined from is not an actual diffusion coefficient. Samples displaying multiple scattering will tend towards smaller sizes since d_H ∝ k_bT/ D_T. The scope of this skew will additionally be greatly subject to concentration so that the evident size will lessen systematically as the signal is dominated by multiple scattering.

Particle-Particle Interactions

A route for decreasing multiple scattering is to reduce the effective pathlength and, as such, the level of sample in the beam path. Nevertheless, removing multiple scattering by employing a shorter pathlength resolves one issue but not the other. Although it is then feasible to take a measurement at extremely high concentrations, this does not reduce the impact of particle-particle interactions.

The decay, or deficiency of correlation, is not artificially fast. However, direct interactions across particles still stop the measurement of a true single particle attribute: particle size. There are numerous important kinds of inter-particle interactions: attraction, clustering, repulsion, or any additional kind of force that can generate coupled motion. Additionally, the true size is not being measured despite having the ability to gain a valid diffusion coefficient.

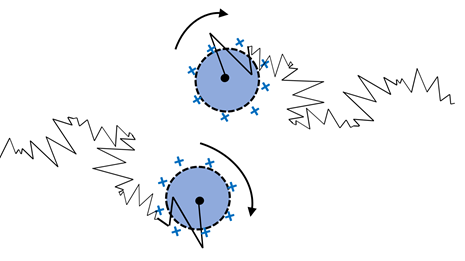
Figure 1.3. One significant and common interaction is charge at the particle surface as shown for positively charged colloidal particles (above) where like-charges cause repulsion between particles. Image Credit: Brookhaven Instrument Corporation

At high concentrations, it is not feasible to overlook the interaction possibilities between particles; if the potential is attractive or repulsive, it still causes the formation of mutual diffusion as the motions of many particles cannot be decoupled. The primary relationship between diffusion coefficient and concentration, c, can be conveyed as D_T (c) = D_o (1+kc), where k is a concentration coefficient that pertains to the power of the interaction. Larger order terms in c may occur, but to acquire D_o, the true self-diffusion coefficient and the true size, extrapolate from the linear region in c.

True Size

What is Dilute Enough? Working in The Dilute Limit.

Serial dilution is an efficient means of ascertaining if a sample is adequately dilute to create a reasonable DLS measurement. As the dilute limit is approached, the apparent particle size meets a limiting, or invariant, hydrodynamic size. As displayed for the subsequent flexible polymers: Sodium Polystyrene Sulfonate (NaPSS) and Polyvinylpyrrolidone (PVP).

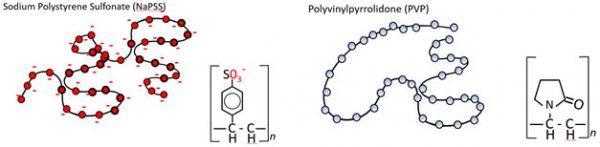
Figure 2.0. The two flexible polymers being compared are NaPSS and PVP. NaPSS has a high linear charge density, due to the presence of permanent negative charges. In contrast, PVP is uncharged. Both samples are of similar M_w and chain length. Image Credit: Brookhaven Instrument Corporation

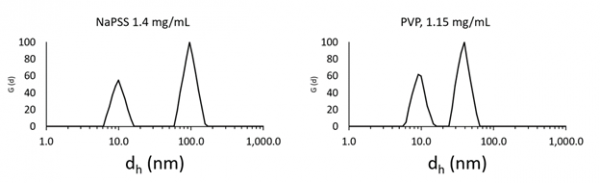
Figure 2.1. Even at high dilution a second mode is observed in the size distribution, with hydrodynamic sizes on the order of 10 nm. Image Credit: Brookhaven Instrument Corporation

Due to its large charge density, NaPSS has very strong particle-particle interactions, stemming from electrostatic repulsion across sidechains. Charting diffusion coefficient as a function of concentration for both polymers provides the following plots:

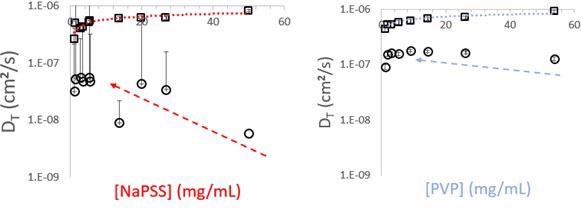
Figure 2.2. Dilution of NaPSS and PVP from starting concentrations of 50 mg/mL continued until the measured diffusion coefficients began to approach constant values. The fast modes, D_T > 1×10^-7 cm²/sec, corresponds to the size of an individual polymer chain. Image Credit: Brookhaven Instrument Corporation

The largest concentrations recorded for each are on the order of 50 mg/mL. Each solution is entirely optically transparent. However, each exhibit signs of multiple scattering and intense particle-particle interactions. Beginning at the largest concentrations, both polymer solutions display bimodal size distributions. The mode relating to the bigger diffusion coefficient slowly moves towards a limiting value as concentration is lessened. The mode relating to the lower diffusion coefficient falls off quickly between 50 mg/mL and around 15 mg/mL. This impact is further distinct for NaPSS, predictable given the increased interaction potential, where high negative linear charge density causes strong repulsive interactions improving inter- and intra- molecular interactions, particularly in contrast to PVP, which is an uncharged linear polymer of similar molecular weight.

Extrapolation of the fast mode to zero concentration provides hydrodynamic diameters nearing 10 nm for PVP and between 10-13 nm for NaPSS, values likely from their individual molecular weights. At the biggest concentrations, each polymer begins above their crucial overlap concentrations, C*, the volume fraction above which polymer chains are no longer spatially removed from one another in solution.

This vital concentration is subject to the molecular weight, chain length and radius of gyration of the polymer chain. Only as the smaller end of the semi-dilute region is neared does the determined hydrodynamic size truly relate to the dimensions of the chains.

Summary

Two key elements affect the capacity to measure particle size at large concentrations: multiple scattering and interparticle interactions. Measurements taken in dilute solution or suspension may be employed to consistently calculate particle size directly.

Even in the absence of multiple scattering, measurements taken in the semi-dilute region do not automatically disclose particle size and as such good care needs to be employed to understand such outcomes. It is also proven that serial dilution can be employed to detect the region in which the sample is suitably dilute to measure.

This information has been sourced, reviewed and adapted from materials provided by Brookhaven Instrument Corporation.

For more information on this source, please visit Brookhaven Instrument Corporation.