Polymer-based dielectrics are widely used in different electrical and electronic devices like capacitors, power transmission cables, and microchips. To adapt to different working conditions, a range of distinct properties like dielectric and thermal parameters are desired for polymers, which can be tuned by customizing the chemical and morphological structure or adding nanofillers/additives to form nanocomposites. This is discussed in the journal IET Nanodielectrics.

Study: Review of machine learning-driven design of polymer-based dielectrics. Image Credit: Michael Traitov/Shutterstock.com
Extensive efforts have been devoted to the design and development of polymer-based dielectrics to optimize their properties. As a result, new paradigms are expected to efficiently design polymer-based dielectrics with desired properties.
The emerging machine learning (ML) technique trained on massive amounts of data establishes linkages between input fingerprints and output properties, which provides a powerful surrogate model for the structure–property linkage analysis.
Moreover, inverse design methods such as evolution searching (ES) strategies and generative models can be employed to explore the large space of potential materials, greatly accelerating the discovery and development of new polymers. Figure 1 illustrates the workflow of ML methods for the rational design of polymer dielectrics.
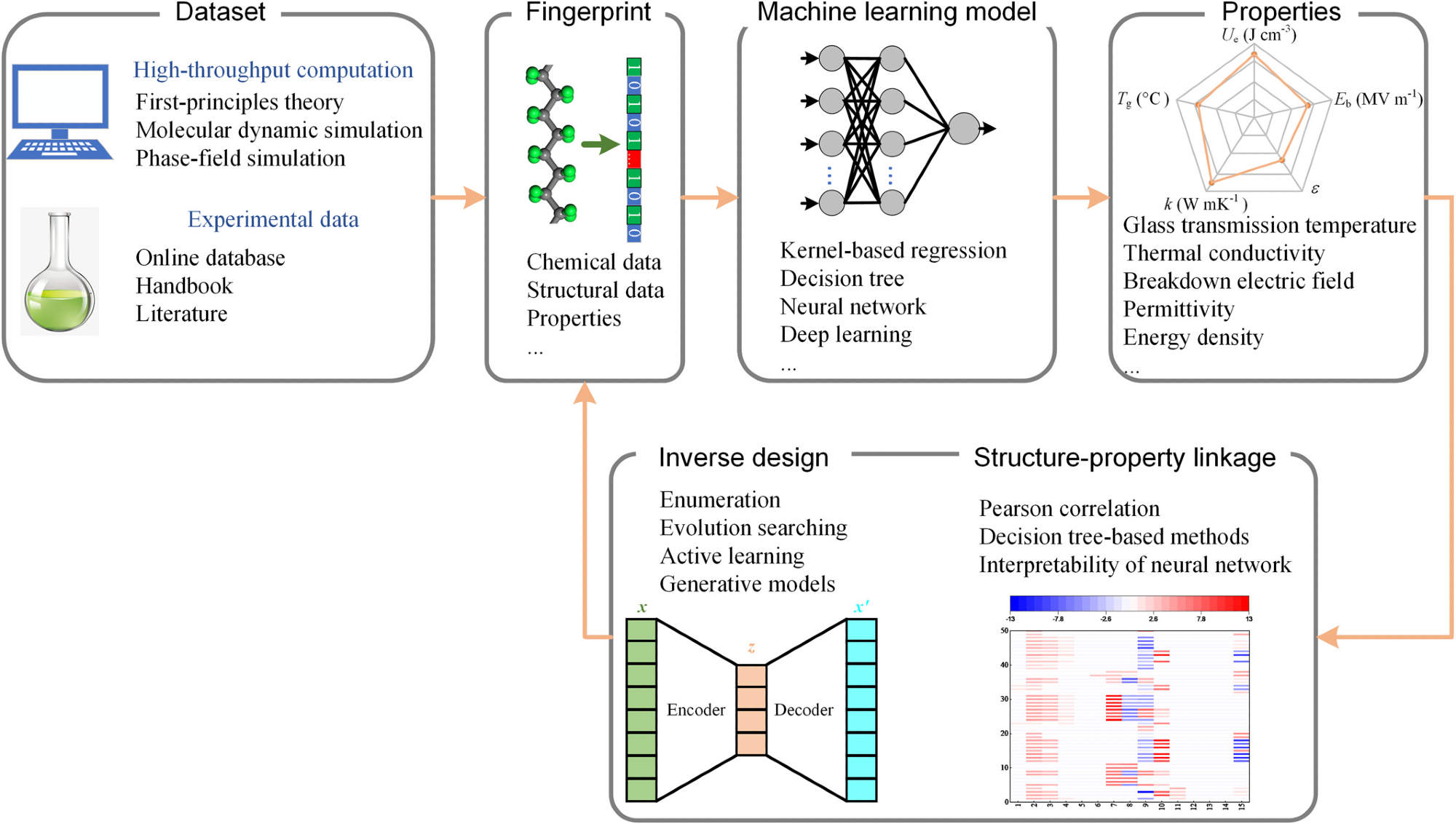
Figure 1. The schematic of machine learning methods for the rational design of polymer-based dielectrics. Image Credit: Zhu, et al., 2021
The study attempted to offer an overview of the application of ML-driven methods for the rational design of polymer or nanocomposite dielectrics.
Methodology
The ML methods employed to design polymer-based dielectrics often involve supervised learning, where the reliability of these models is mainly governed by the amount and quality of samples in the training dataset. The key sources of training data are online libraries, high-throughput computations, and experiments.
As an effective alternative approach, high-throughput computations that involve first-principles theory, phase-filed model, molecular dynamics (MD), and finite-element method have been used to obtain property data. The researchers illustrate the DFT method used to estimate the charge injection barrier from the electrode to polymer and the trap depth in polymer, respectively.
The thermodynamic properties of nanocomposites or polymers, such as thermal conductivity and glass transmission temperature, can be readily calculated through MD simulations. For instance, the non-equilibrium MD has been extensively used to estimate thermal conductivity.
Phase-field models have been created to analyze the breakdown behavior and effective permittivity of polymer nanocomposites (Figure 2e), where the effect of the microstructure of nanocomposites, like the shape and orientation of nanofillers, can be considered.
ML-driven approaches involve two different steps: numerically representing the materials in the dataset (fingerprinting) and establishing a mapping between the target property and the fingerprinted input (learning).
The polymers were fingerprinted through the occurrence of various kinds of building fragments (including blocks like CO, CH2, CS, C6H4, O, C4H2S, and NH) in terms of their number fractions.
The aim of the ML algorithm is to establish a mapping between the target property and the fingerprinted input, which offers an effective surrogate for calculating the target property. At present, linear and non-linear regression algorithms are being used to build the model, of which artificial neural networks (ANNs) and kernel-based regression are the most popular algorithms.
Gaussian process regression (GPR) is a well-established method for developing ML models for polymer dielectrics. The mean and variance for objective values can be well estimated based on the calculation of the covariance matrix, the elements of which indicate the covariance between two features.
Different ML algorithms can be used for developing a surrogate model between the target property and the fingerprinted input. These techniques have their own benefits and drawbacks in terms of the size of applicable dataset, computational efficiency, and prediction capabilities. Table 1 depicts a brief comparison of these algorithms.
Table 1. Comparison of different ML algorithms. Source: Zhu, et al., 2021
| ML algorithm |
Advantages |
Disadvantages |
| Linear regression |
Simplest method |
Neglect of non-linear linkage between descriptors and properties |
| KRR, SVM |
Low computational cost |
Unfeasible for large datasets as the size of the kernel matrix scales quadratically with the number of features |
| GPR |
The uncertainty for objective values can be well predicted |
Requires a manageable dataset size and does not have the capability to train multiple properties in one single model |
| RF |
Feasible for large datasets and provides an intrinsic metric to evaluate the importance of each descriptor |
Might create over-complex trees and cause overfitting |
| ANN |
Exhibits strong ability to capture non-linear complex relations from large-scale datasets |
Requires much more training data, is time-consuming, and lacks interpretability; also called ‘black boxes’. |
Deep
neural
network |
Feasible for graphical representations of materials and learns representations with different abstraction levels |
Requires much more training data, is time-consuming, and lacks interpretability |
Abbreviations: ANN, artificial neural network; GPR, Gaussian process regression; KRR, kernel ridge regression; ML, machine learning; RF, random forest; SVM, support vector machine.
A GPR-based ML model was employed to screen potential polymer nanocomposites with desired breakdown strength, permittivity, and energy density, leading to different kinds of nanocomposites with preferred properties.
Active learning algorithms that iteratively fill the chosen optimal point into the training dataset were shown to be effective in materials design.
Active learning algorithms include three interwoven steps: (1) training the ML-based surrogate model for predicting the target property, (2) choosing the optimal sample based on the prediction results such as values and uncertainties, and (3) supplementing the most ideal sample into the training dataset.
Pure exploration, pure exploitation, and balanced exploration and exploitation principles were used to choose the most ideal sample.
The GA method was used in tandem with ML models to develop polymers with a large bandgap and high glass transition temperature. An inverse design by PSO and trained ML algorithm was demonstrated, estimating 17 polymer structures from user-defined cloud points.
In the case of an autoencoder, the encoder figures out how to map the polymers to a lower-dimension space called the latent space, and the decoder tries to regain the original representation from the latent space. For GAN, the generator tries to produce samples from a distribution, while the discriminator forecasts whether the probability of a data is real or synthetic.
Pearson correlation coefficients (PCCs) between different target properties and features can be estimated to represent the variable importance, where PCC with −1 represents high negative correlations and 1 represents high positive correlations.
CNN gradient analysis was used to identify the composition–structure–property relationships for an array of BiVO4 alloys. DeepLIFT was applied to probe the contribution of various molecular structures to thermal conductivity of polymer chains.
Applications
Polymer-based dielectrics have found extensive applications in different electrical and electronic devices. It has been shown that the ML-driven approach is an effective means for rationally designing polymer-based dielectrics.
Table 2 summarizes certain examples of the ML-driven approach used to design polymers and nanocomposites, where the fingerprints, target properties, data sources, inverse design techniques, and ML models are provided.
Table 2. Some examples of the ML-driven approach applied in designing polymers and nanocomposites. Source: Zhu, et al., 2021
Target
property |
Data
source |
Fingerprint |
ML
model |
Inverse
design
method |
Reference |
| Polymers: Bandgap of the polymer and electron injection barrier (proxies for breakdown strength) |
DFT computation |
Hierarchical fingerprint in [53] |
GPR |
Enumeration |
[53] |
| SMILES in [43] |
[43] |
Polymers: Bandgap and dielectric constant (proxies
for energy density) |
DFT computation |
Fingerprints based on singles, doubles and triples components |
KRR |
Enumeration |
[22] |
| Polymers: Frequency-dependent dielectric constant |
Experimental data in
studies |
Hierarchical fingerprint |
GPR |
Enumeration |
[34] |
| Polymers: Dielectric constant |
Experimental data in
studies |
Hierarchical fingerprint |
Interval support vector regression |
- |
[86] |
| Polymers: Bandgap, glass transition temperature |
Experimental data in
studies |
SMILES |
GPR |
GA in [102] |
[102] |
| VAE in [104] |
[104] |
| Polymers: Glass transition temperature |
Experimental data in
studies |
SMILES |
GPR |
Active learning |
[88] |
| Polymers: Specific heat of polymers |
Experimental data |
Hierarchical fingerprint constructed using the Materials Studio software |
Decision tree |
- |
[66] |
| Polymers: Thermal conductivity |
MD simulations |
SMILES |
CNN |
- |
[25] |
| Polymers: Thermal conductivity |
Online database |
SMILES |
Bayesian method |
Enumeration |
[39] |
| Nanocomposites: Breakdown strength, permittivity and energy density |
Experimental data in
studies |
Descriptor-based fingerprint |
GPR |
Enumeration |
[26] |
| Nanocomposites: Breakdown strength |
Monte Carlo multi-scale simulation |
MCR methods |
GPR |
GA |
[79] |
| Nanocomposites: Energy density |
Phase-field simulations |
Descriptor-based fingerprint |
NN |
Enumeration |
[60] |
Nanocomposites: Thermal
conductivity |
FEM simulation |
2D cross-sectional
images |
CNN |
- |
[61] |
Abbreviations: CNN, convolutional neural network; DFT, density functional theory; FEM, finite-element model; GA, genetic algorithm; GPR, Gaussian process regression; KRR, kernel ridge regression; MCR, microstructure characterization and reconstruction MD, molecular dynamic; ML, machine learning; NN, neural network; SMILES, Simplified Molecular-Input Line-Entry System; VAE, variational autoencoder.
Conclusion
The ML-driven approach trained on enormous amounts of data has been demonstrated to be a robust technique for structure–property linkage analysis and the quick design of polymer-based dielectrics. The training data were largely gathered from online polymer libraries, high-throughput computations, and experiments in the literature.
Increasing knowledge of the connection between microstructures of polymers/nanocomposites and preferred properties should make way for incorporating other vital descriptors like the morphologies, trap state, and processing conditions to more precisely estimate the dielectric properties.
More sophisticated inverse design methods and neural network algorithms can be used for structure–property analysis, polymer dielectrics discovery, and property prediction.
Journal Reference:
Zhu, M.-X., Deng, T., Dong, L., Chen, J.-M., Dang, Z.-M. (2021) Review of machine learning-driven design of polymer-based dielectrics. IET Nanodielectrics. doi.org/10.1049/nde2.12029.
References and Further Reading
Dang, Z.-M., et al. (2013) Flexible nanodielectric materials with high permittivity for power energy storage. Advanced Materials, 25, pp. 6334–6365. doi.org/10.1002/adma.201301752.
Li, H., et al. (2021) Dielectric polymers for high‐temperature capacitive energy storage. Chemical Society Reviews, 50, pp. 6369–6400. doi.org/10.1039/D0CS00765J.
Li, Z & Du, B (2018) Polymeric insulation for high‐voltage DC extruded cables: challenges and development directions. IEEE Electrical Insulation Magazine, 34(6), pp. 30–43. doi.org/10.1109/MEI.2018.8507715.
Montanari, G. C., et al. (2018) Next generation polymeric high voltage direct current cables—a quantum leap needed? IEEE Electrical Insulation Magazine, 34(2), pp. 24–31. doi.org/10.1109/MEI.2018.8300441.
Burger, N., et al. (2016) Review of thermal conductivity in composites: mechanisms, parameters and theory. Progress in Polymer Science, 61, pp. 1–28. doi.org/10.1016/j.progpolymsci.2016.05.001.
Huang, C., et al. (2018) Thermal conductivity of polymers and polymer nanocomposites. Materials Science and Engineering: R: Reports, 132, pp. 1–22. doi.org/10.1016/j.mser.2018.06.002.
Yuan, C., et al. (2020) Polymer/molecular semiconductor all-organic composites for high-temperature dielectric energy storage. Nature Communications, 11, p. 3919. doi.org/10.1038/s41467-020-17760-x.
Zhang, C., et al. Grafting of antioxidant onto polyethylene to improve DC dielectric and thermal aging properties. IEEE Transactions on Dielectrics and Electrical Insulation, 28(2), pp. 541–549. doi.org/10.1109/TDEI.2020.009261.
Tanaka, T., et al. (2004) Polymer nanocomposites as dielectrics and electrical insulation‐perspectives for processing technologies, material characterization and future applications. IEEE Transactions on Dielectrics and Electrical Insulation, 11(5), pp. 763–784. doi.org/10.1109/TDEI.2004.1349782.
Huang, X., et al. (2019) High‐k polymer nanocomposites with 1D filler for dielectric and energy storage applications. Progress in Materials Science, 100, pp. 187–225. doi.org/10.1016/j.pmatsci.2018.10.003.
Jiang, J., et al. (2019) Polymer nanocomposites with interpenetrating gradient structure exhibiting ultrahigh discharge efficiency and energy density. Advanced Energy Materials, 9 (15), p. 1803411. doi.org/10.1002/aenm.201803411.
Mannodi‐Kanakkithodi, A., et al. (2016) Rational co‐design of polymer dielectrics for energy storage. Advanced Materials, 28(30), pp. 6277–6291. doi.org/10.1002/adma.201600377.
Le, T., et al. (2012) Quantitative structure–property relationship modeling of diverse materials properties. Chemical Reviews, 112, pp. 2889–2919. doi.org/10.1021/cr200066h.
Liu, Y., et al. (2020) Machine learning assisted materials design and discovery for rechargeable batteries. Energy Storage Materials, 31, pp. 434–450. doi.org/10.1016/j.ensm.2020.06.033.
Doan Tran, H., et al. (2020) Machine‐learning predictions of polymer properties with Polymer Genome. Journal of Applied Physics, 128, pp. 171104. doi.org/10.1063/5.0023759.
Zhou, T., et al. (2019) Big data creates new opportunities for materials research: a review on methods and applications of machine learning for materials design. Engineering, 5(6), pp. 981–1192. doi.org/10.1016/j.eng.2019.02.011.
Butler, K. T., et al. (2018) Machine learning for molecular and materials science. Nature, 559(7715), pp. 547–555. doi.org/10.1038/s41586-018-0337-2.
Kumar, J. N., et al. (2019) Challenges and opportunities of polymer design with machine learning and high throughput experimentation. MRS Communications, 9(2), pp. 537–544. doi.org/10.1557/mrc.2019.54.
Sha, W., et al. (2021) Machine learning in polymer informatics. InfoMat, 3(4), pp. 353–361. doi.org/10.1002/inf2.12167.
Jackson, N. E., et al. (2019) Recent advances in machine learning towards multiscale soft materials design. Current Opinion in Chemical Engineering, 23, pp. 106–114. doi.org/10.1016/j.coche.2019.03.005.
Sanchez‐Lengeling, B & Aspuru‐Guzik, A (2018) Inverse molecular design using machine learning: generative models for matter engineering. Science, 361, pp. 360–365. doi.org/10.1126/science.aat2663.
Mannodi‐Kanakkithodi, A., et al. (2016) Machine learning strategy for accelerated design of polymer dielectrics. Scientific Reports, 6, p. 20952. doi.org/10.1038/srep20952.
Sharma, V., et al. (2014) Rational design of all organic polymer dielectrics. Nature Communications, 5, p. 4845. doi.org/10.1038/ncomms5845.
Shen, Z.‐H., et al. (2019) Phase‐field modeling and machine learning of electric‐thermal‐mechanical breakdown of polymer‐based dielectrics. Nature Communications, 10, pp. 1843. doi.org/10.1038/s41467-019-09874-8.
Zhu, M.‐X., et al. (2020) Machine-learning-driven discovery of polymers molecular structures with high thermal conductivity. International Journal of Heat and Mass Transfer, 162, p. 120381. doi.org/10.1016/j.ijheatmasstransfer.2020.120381.
Zhu, M.‐X., et al. (2021) Rational design of high‐energy‐density polymer composites by machine learning approach. ACS Applied Energy Materials, 4(2), pp. 1449–1458. doi.org/10.1021/acsaem.0c02647.
Wan, X., et al. (2019) Materials discovery and properties prediction in thermal transport via materials informatics: a mini‐review. Nano Letters, 9(6), pp. 3387–3395. doi.org/10.1021/acs.nanolett.8b05196.
Balachandran, P V (2019) Machine learning guided design of functional materials with targeted properties. Computational Materials Science, 164(15), 82–90. doi.org/10.1016/j.commatsci.2019.03.057.
Mannodi‐Kanakkithodi, A., et al. (2018) Scoping the polymer genome: a roadmap for rational polymer dielectrics design and beyond. Materials Today, 21(7), pp. 785–796. doi.org/10.1016/j.mattod.2017.11.021.
Meredig, B., et al. (2014) Combinatorial screening for new materials in unconstrained composition space with machine learning. Physical Review B, 89, p. 094104. doi.org/10.1103/PhysRevB.89.094104.
Ramprasad, R., et al. (2017) Machine learning in materials informatics: recent applications and prospects. npj Computational Materials, 3, p. 54. doi.org/10.1038/s41524-017-0056-5.
Schmidt, J., et al. (2019) Recent advances and applications of machine learning in solid‐state materials science. npj Computational Materials, 5, 83. doi.org/10.1038/s41524-019-0221-0.
Chen, L., et al. (2021) Polymer informatics: current status and critical next steps. Materials Science and Engineering: R: Reports, 144, p. 100595. doi.org/10.1016/j.mser.2020.100595.
Chen, L., et al. (2020) Frequency‐dependent dielectric constant prediction of polymers using machine learning. npj Computational Materials, 6, 61. doi.org/10.1038/s41524-020-0333-6.
Otsuka, S., et al. (2011) Polyinfo: polymer database for polymeric materials design. In: Fatos, X., Leonard, B., Nik, B. (eds.) International Conference on Emerging Intelligent Data and Web Technologies, Tirana, Albania, September. pp. 22–29. IEEE, Los Alamitos.
CROW (2015) Polymer Properties Database [Internet]. Available at: http://www.polymerdatabase.com (Accessed 10 October 2021).
The Center for Hierarchical Materials Design (CHiMaD) (2015). Polymer Property Predictor and Database [Internet]. Available at: https://pppdb.uchicago.edu (Accessed 10 October 2021).
Huan, T. D., et al. (2016) A polymer dataset for accelerated property prediction and design. Scientific Data, 3, p. 160012. doi.org/10.1038/sdata.2016.12.
Wu, S., et al. (2019) Machine‐learning‐assisted discovery of polymers with high thermal conductivity using a molecular design algorithm. npj Computational Materials, 5, p. 66 doi.org/10.1038/s41524-019-0203-2.
Zhao, H., et al. (2018) NanoMine schema: an extensible data representation for polymer nanocomposites. APL Materials, 6, p. 111108. doi.org/10.1063/1.5046839.
Tshitoyan, V., et al. (2019) Unsupervised word embeddings capture latent knowledge from materials science literature. Nature, 571, pp. 95–98. doi.org/10.1038/s41586-019-1335-8.
Kim, E., et al. (2017) Materials synthesis insights from scientific literature via text extraction and machine learning. Chemical Materials, 29, pp. 9436–9444. doi.org/10.1021/acs.chemmater.7b03500.
Kamal, D., et al. (2020) Computable bulk and interfacial electronic structure features as proxies for dielectric breakdown of polymers. ACS Applied Materials & Interfaces, 12(33), pp. 37182–37187. doi.org/10.1021/acsami.0c09555.
Wang, W., et al. (2019) Interfacial charge dynamics of cross‐linked polyethylene/ethylene‐propylene‐diene dual dielectric polymer as revealed by energy band structure. IEEE Transactions on Dielectrics and Electrical Insulation, 26(6), pp. 1755–1762. doi.org/10.1109/TDEI.2019.008122.
Zhang, T., et al. (2014) Polymer nanofibers with outstanding thermal conductivity and thermal stability: fundamental linkage between molecular characteristics and macroscopic thermal properties. The Journal of Physical Chemistry C, 118(36), pp. 21148–21159. doi.org/10.1021/jp5051639.
Shen, Z.‐H., et al. (2017) High‐throughput phase‐field design of high‐energy‐density polymer nanocomposites. Advanced Materials, 30(2), p. 1704380. doi.org/10.1002/adma.201704380.
Wang, C. C., et al. (2014) Computational strategies for polymer dielectrics design. Polymer, 55, pp. 979–988. doi.org/10.1016/j.polymer.2013.12.069.
Zhu, J., et al. (2020) Rational design of heat‐resistant polymers with low curing energies by a materials genome approach. Chemical Materials, 32(11), pp. 4527–4535. doi.org/10.1021/acs.chemmater.0c00238.
Chen, X., et al. (2019) First‐principle investigation of the charge injection barriers of polyethylene and polytetrafluoroethylene oligomers. Journal of Applied Physics, 126, p. 035101. doi.org/10.1063/1.5089863.
Sato, M., et al. (2017) First‐principles studies of carrier injection in polyethylene (PE) and ethylene‐vinyl acetate copolymer (EVA) oligomers. IEEE Transactions on Dielectrics and Electrical Insulation, 24(1), pp. 574–582. doi.org/10.1109/TDEI.2016.006346.
Meunier, M., et al. (2001) Molecular modeling of electron traps in polymer insulators: chemical defects and impurities, The Journal of Chemical Physics, 115, pp. 2876–2881. doi.org/10.1063/1.1385160.
Takada, T., et al. (2015) Determination of charge‐trapping sites in saturated and aromatic polymers by quantum chemical calculation. IEEE Transactions on Dielectrics and Electrical Insulation, 22(2), pp. 1240–1249. doi.org/10.1109/TDEI.2015.7076827.
Kamal, D., et al. (2021) Novel high voltage polymer insulators using computational and data‐driven techniques. The Journal of Chemical Physics, 154, p. 174906. doi.org/10.1063/5.0044306.
Wen, C., et al. (2020) Determination of glass transition temperature of polyimides from atomistic molecular dynamics simulations and machine‐learning algorithms. Journal of Polymer Science, 58(11), pp. 1521–1534. doi.org/10.1002/pol.20200050.
Qin, H., et al. (2019) Thermal transport in graphene‐based layered materials: an analytical model validated with extensive molecular dynamics simulations. Carbon, 155, pp. 114–121. doi.org/10.1016/j.carbon.2019.08.062.
Shen, Z.-H., et al. (2018) Phase‐field model of electrothermal breakdown in flexible high‐temperature nanocomposites under extreme conditions, Advanced Energy Materials. 8(20), pp. 1800509. doi.org/10.1002/aenm.201800509.
Zhu, M.‐X., et al. (2020) Phase‐field modeling of electric‐thermal breakdown in polymers under alternating voltage. IEEE Transactions on Dielectrics and Electrical Insulation, 27(4), pp. 1128–1135. doi.org/10.1109/TDEI.2020.008717.
Roy, S. L., et al. (2006) Description of charge transport in polyethylene using a fluid model with a constant mobility: fitting model and experiments. Journal of Physics D Applied Physics, 39, pp. 1427–1436. doi.org/10.1088/0022-3727/39/7/014.
Chen, J., et al. (2020) Space charge dynamics in double‐layered insulation cable under polarity reversal voltage. IEEE Transactions on Dielectrics and Electrical Insulation, 27(2), pp. 622–630. doi.org/10.1109/TDEI.2019.008457.
Shen, Z.‐H., et al. (2021) Designing polymer nanocomposites with high energy density using machine learning. npj Computational Materials, 7, p. 110. doi.org/10.1038/s41524-021-00578-6.
Rong, Q., et al. (2019) Predicting the effective thermal conductivity of composites from cross sections images using deep learning methods. Composites Science and Technology, 184(10), p.107861. doi.org/10.1016/j.compscitech.2019.107861.
Li, S., et al. (2019) Understanding insulation failure of nanodielectrics: tailoring carrier energy. High Voltage, 5(6), 643–649. doi.org/10.1049/hve.2019.0122.
Huang, Y., et al. (2017) Predicting the breakdown strength and lifetime of nanocomposites using a multi‐scale modeling approach. Journal of Applied Physics, 122, p. 065101. doi.org/10.1063/1.4997720.
Van Krevelen, D (2009) Properties of Polymers: Their Correlation With Chemical Structure; Their Numerical Estimation and Prediction From Additive Group Contributions. Elsevier Science.
Bicerano, J (2002) Prediction of Polymer Properties. CRC Press.
Bhowmik, R., et al. (2021) Prediction of the specific heat of polymers from experimental data and machine learning methods. Polymer, 220, p. 123558. doi.org/10.1016/j.polymer.2021.123558.
Kim, C., et al. (2018) Polymer genome: a data‐powered polymer informatics platform for property predictions. Journal of Physical Chemistry C, 122, pp. 17575–17585. doi.org/10.1021/acs.jpcc.8b02913.
Chen, D., et al. (2018) Designing disordered hyperuniform two‐phase materials with novel physical properties. Acta Materialia, 142, pp. 152–161 doi.org/10.1016/j.actamat.2017.09.053.
Weininger, D (1988) SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. Journal of Chemical Information and Modeling, 28(1), pp. 31–36. doi.org/10.1021/ci00057a005.
Weininger, D (1989) SMILES. 2. Algorithm for generation of unique SMILES notation. Journal of Chemical Information and Modeling, 29, pp. 97–101. doi.org/10.1021/ci00062a008.
Lin, T. S., et al. (2019) BigSMILES: a structurally‐based line notation for describing macromolecules. ACS Central Science, 5, pp. 1523–1531.
Yan, C., et al. (2020) Machine learning assisted discovery of new thermoset shape memory polymers based on a small training dataset. Polymer, 214, p. 123351. doi.org/10.1016/j.polymer.2020.123351.
Rogers, D & Hahn, M (2010). Extended‐connectivity fingerprints. Journal of Chemical Information and Modeling, 50(5), pp. 742–754.
Rdkit (2012) Open source toolkit for cheminformatics. Available at: https://www.rdkit.org/ (Accessed 10 October 2021).
Fetanat, M., et al. (2021) Machine learning for advanced design of nanocomposite ultrafiltration membranes. Industrial & Engineering Chemistry Research, 60, pp. 5236–5250. doi.org/10.1021/acs.iecr.0c05446.
Xu, H., et al. (2014) descriptor‐based design methodology for developing heterogeneous microstructural materials system. Journal of Mechanical Design, 136, p. 051007 doi.org/10.1115/1.4026649.
Wei, H., et al. (2018) Predicting the effective thermal conductivities of composite materials and porous media by machine learning methods. International Journal of Heat and Mass Transfer, 127, pp. 908–916. doi.org/10.1016/j.ijheatmasstransfer.2018.08.082.
Yang, Z., et al. (2018) Deep learning approaches for mining structure‐property linkages in high contrast composites from simulation datasets. Materials Science, 151, pp. 278–287. doi.org/10.1016/j.ijheatmasstransfer.2018.08.082.
Schadler, L. S., et al. (2020) A perspective on the data‐driven design of polymer nanodielectrics. Journal of Physics D: Applied Physics, 53, p. 333001. doi.org/10.1088/1361-6463/ab8b01.
Jiao, Y., et al. (2009) superior descriptor of random textures and its predictive capacity. Proceedings of the National Academy of Sciences, 106 (42), pp. 17634–17639 doi.org/10.1073/pnas.0905919106.
Torquato, S., et al. (1988) Two‐point cluster function for continuum percolation. The Journal of Chemical Physics, 88(10), pp. 6540–6547. doi.org/10.1063/1.454440.
Ghumman, U.F., et al. (2018) A spectral density function approach for active layer design of organic photovoltaic cells. Journal of Mechanical Design, 140, p. 111408. doi.org/10.1115/1.4040912.
Chen, A., et al. (2020) Machine learning: accelerating materials development for energy storage and conversion. InfoMat, 2, pp. 553–576. doi.org/10.1002/inf2.12094.
Zhou, Z., et al. (2021) Journal of Materials Chemistry A and Materials Advances Editor's choice web collection: Machine learning for materials innovation. Materials Chemistry, 9, pp. 1295–1296. doi.org/10.1039/D0MA90054K.
Boser, B. E., et al. (1992) A training algorithm for optimal margin classifiers. In: Haussler, D. (Ed.) Proceedings of the Fifth Annual Workshop on Computational Learning Theory (COLT’92), Pittsburgh, pp. 144–152. ACM Press, New York.
Yi, Y., et al. (2021) Interval support vector regression enables high‐throughput machine learning predictions for dielectric constant of polymer dielectrics. Applied Physics Letters, 118, p.223901. doi.org/10.1063/5.0046854.
Deisenroth, M P & Ng, J W (2015) Distributed Gaussian processes. In: Bach, F & Blei, D (Eds) ICML’15 Proceedings of the 32nd International Conference on Machine Learning, July, Vol. 37, pp. 1481–1490.
Kim, C., et al. (2019) Active‐learning and materials design: the example of high glass transition temperature polymers. MRS Communications, 9(3), pp. 860–866. doi.org/10.1557/mrc.2019.78.
Patra, A., et al. (2020) A multi‐fidelity information‐fusion approach to machine learn and predict polymer bandgap. Computational Materials Science, 171, p. 109286 doi.org/10.1016/j.commatsci.2019.109286.
Quinlan, J (1987) Simplifying decision trees. International Journal of Man-Machine Studies, 27, pp. 221–234. doi.org/10.1016/S0020-7373(87)80053-6.
Breiman, L (2001) Random forests. Machine Learning, 45, pp. 5–32.
Liang, J., et al. (2021) Machine‐learning‐assisted low dielectric constant polymer discovery. Materials Chemistry Frontiers, 5, pp. 3823–3829. doi.org/10.1039/D0QM01093F.
Mannodi‐Kanakkithodi, A., et al. (2016) Critical assessment of regression‐based machine learning methods for polymer dielectrics. Computational Materials Science, 125, pp. 123–135. doi.org/10.1016/j.commatsci.2016.08.039.
Goh, G. B., et al. (2017) Deep learning for computational chemistry. Journal of Computational Chemistry, 38(16), 1291–1307. doi.org/10.1002/jcc.24764.
Yang, H., et al. (2018) Machine learning and artificial neural network prediction of interfacial thermal resistance between graphene and hexagonal boron nitride. Nanoscale, 10, pp. 19092–19099. doi.org/10.1039/C8NR05703F.
Nazarova, A. L., et al. (2021) Dielectric polymer property prediction using recurrent neural networks with optimizations. Journal of Chemical Information and Modeling, 61, pp. 2175–2186. doi.org/10.1021/acs.jcim.0c01366.
LeCun, Y., et al. (2019) Deep learning. Nature, 521, 436–444. doi.org/10.1038/nature14539.
Agrawal, A & Choudhary, A (2019) Deep materials informatics: applications of deep learning in materials science. MRS Communications, 9, pp. 779–792. doi.org/10.1557/mrc.2019.73.
Chandrasekaran, A., et al. (2020) A deep learning solvent-selection paradigm powered by a massive solvent/nonsolvent database for polymers. Macromolecules, 53(12), pp. 4764–4769. doi.org/10.1021/acs.macromol.0c00251.
Chen, G., et al. (2021) Predicting polymers’ glass transition temperature by a chemical language processing model. Polymers, 13, p. 1898. doi.org/10.3390/polym13111898.
Dong, Y., et al. (2019) Bandgap prediction by deep learning in configurationally hybridized graphene and boron nitride. npj Computational Materials, 5, p. 26. doi.org/10.1038/s41524-019-0165-4.
Kim, C., et al. (2021) Polymer design using genetic algorithm and machine learning. Computational Materials Science, 186, p. 110067. doi.org/10.1016/j.commatsci.2020.110067.
Kumar, J. N., et al. (2019) Machine learning enables polymer cloud-point engineering via inverse design. npj Computational Materials, 5, p. 73. doi.org/10.1038/s41524-019-0209-9.
Batra, R., et al. (2020) Polymers for extreme conditions designed using syntax-directed variational autoencoders. Chemistry of Materials, 32, pp. 10489–10500. doi.org/10.1021/acs.chemmater.0c03332.
Balachandran, P. V., et al. (2016) Adaptive strategies for materials design using uncertainties. Scientific Reports, 6, p. 19660. doi.org/10.1038/srep19660.
Jennings, P. C., et al. (2019) Genetic algorithms for computational materials discovery accelerated by machine learning. npj Computational Materials, 5, p. 46. doi.org/10.1038/s41524-019-0181-4.
Wei, H., et al. (2020) Genetic algorithm-driven discovery of unexpected thermal conductivity enhancement by disorder. Nano Energy, 71, p. 104619. doi.org/10.1016/j.nanoen.2020.104619.
Kingma, D P & Welling, M (2013) Auto-encoding variational Bayes. arXiv:1312.6114v10 [stat.ML].
Kusner, M. J., et al. (2017) Grammar variational autoencoder. arXiv:1703.01925 [stat.ML].
Dai, H., et al. (2018) Syntax-directed variational autoencoder for structured data. arXiv:1802.08786 [cs.LG].
Arjovsky, M., et al. (2017) Wasserstein GAN. arXiv:1701.07875 [stat.ML].
Hjelm, R. D., et al. (2017) Boundary-seeking generative adversarial networks. arXiv:1702.08431 [stat.ML].
Santosa, F & Symes, W W (1986) Linear inversion of band-limited reflection seismograms. SIAM Journal on Scientific and Statistical Computing, 7, pp. 1307–1330. doi.org/10.1137/0907087.
Tibshirani, R (1996) Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58, pp. 267–288. doi.org/10.1111/j.2517-6161.1996.tb02080.x.
Kim, C., et al. (2016) From organized high-throughput data to phenomenological theory using machine learning: the example of dielectric breakdown. Chemistry of Materials, 28, pp. 1304–1311. doi.org/10.1021/acs.chemmater.5b04109.
Ouyang, R., et al. (2018) SISSO: A compressed-sensing method for identifying the best low-dimensional descriptor in an immensity of offered candidates. Physical Review Materials, 2, p. 083802. doi.org/10.1103/PhysRevMaterials.2.083802.
Matos, C. R. S., et al. (2007) Principal component analysis of X-ray diffraction patterns to yield morphological classification of brucite particles. Analytical Chemistry, 79, pp. 2091–2095. doi.org/10.1021/ac061991n.
Xu, P., et al. (2021) Machine learning aided design of polymer with targeted band gap based on DFT computation. The Journal of Physical Chemistry B, 125, pp. 601–611. doi.org/10.1021/acs.jpcb.0c08674.
Umehara, M., et al. (2019) Analyzing machine learning models to accelerate generation of fundamental materials insights. npj Computational Materials, 5, p. 34. doi.org/10.1038/s41524-019-0172-5.
Stanev, V., et al. (2018) Machine learning modeling of superconducting critical temperature. npj Computational Materials, 4, p. 29. doi.org/10.1038/s41524-018-0085-8.
Guidotti, R., et al. (2018) A survey of methods for explaining black box models. arXiv:1802.01933v3 [cs.CY].
Shrikumar, A., et al. (2019) Learning important features through propagating activation differences. arXiv:1704.02685v2 [cs.CV].
Lundberg, S M & Lee, S (2017) A unified approach to interpreting model predictions. arXiv:1705.07874v2 [cs.AI].
Ribeiro, M. T., et al. (2016) Why should I trust you? Explaining the predictions of any classifier. arXiv:1602.04938v3 [cs.LG].