Particle characterization involves analyzing particles based on attributes such as shape, size, surface properties, charge properties, mechanical properties, and microstructure, among others. A wide range of commercially available techniques can be used to measure particulate samples.
Size and shape are critical attributes that influence the behavior of particulate substances. Spherical particles can often be characterized by a single-size measurement, such as diameter.
Irregular shapes, however, are more complex to characterize due to their multi-dimensional structure. For example, powders used in manufacturing often require multiple measurement parameters to assess flowability, packing, and other performance characteristics.
Particle size and particle shape analysis are techniques used to measure and report the distribution of sizes and shapes within a sample. These methods are essential for quality control across various industries, including paints, building materials, pharmaceuticals, food production, and toners.
Irregular shapes, however, are more complex to characterize due to their multi-dimensional structure. For example, powders used in manufacturing often require multiple measurement parameters to assess flowability, packing, and other performance characteristics.
Statistical results are often presented as histograms, as they effectively illustrate the distribution of size and shape data, which are inherently statistical due to the large number of particles analyzed. Histograms provide a clear visualization of these distributions, using key measures such as averages and spreads to summarize the data with just a few essential numbers.
Particle shape can significantly impact size.
Particle Size and Particle Shape are critical factors that influence particulate behavior, including flowability, compaction, and mixing. Spherical particles can often be characterized effectively using size-only techniques. However, irregular particles require additional shape measurements to accurately characterize their behavior and predict how they will perform.
Highly irregular particles are particularly challenging to analyze. For raw materials in manufacturing, particle size alone is insufficient to fully understand particle behavior.
Additional shape parameters must be measured, and tools that utilize these parameters are essential for predicting performance. The specific shape measurements required will depend on the irregularity of the particles and their application in final products, helping to achieve better understanding, control, and optimization.
Dynamic image analysis is becoming increasingly prevalent as a complementary evaluative approach because end users are starting to understand the significance of vast data for large sample populations.
A statistical histogram is the first and most fundamental report of any particle shape and size analysis, ideal for viewing channelized data in number- and volume-weighted distributions.
Distribution Histograms
To demonstrate the statistical results from sample analysis, data is grouped into small categories or “bins,” with the number of particles in each size bin reported. Size data can be shown in volume, number, and surface-area weighted histograms, each providing valuable insights into the sample.
As dynamic image analysis is a numerical tool, meaning each particle is recognized and assessed separately, statistical histograms are extremely accurate in each size bin. In dynamic imaging systems, operators can accurately observe the number of particles allocated in each size bin.
As an imaging system, the operator can also view thumbnail images of each particle, providing objective evidence of what is being measured. Size data is typically displayed graphically on a logarithmic scale. Shape and size histograms are often employed to compare variations across sample batches.
Three particle-size histograms are shown below. Despite all looking different, these histograms come from the same sample. Operators should always observe at least the number-weighted and volume-weighted distribution.
Number-weighted distributions are crucial for viewing very fine particles in a sample. Very fine particles can affect a procedure where filtration can be blocked easily. In some cases, fine particles are essential as they assist in lubricating particle movement and flowability.
Fine particle presence can be good or bad depending on the use case, and number-weighted distributions should always be reviewed.
A volume-weighted statistical histogram is detailed below. Volume-weighted distributions are crucial for monitoring large particle presence.
Similarly to fine particles, large particles may be good or bad, so observing volume-weighted statistical distributions is also vital. Surface area weighted distributions are occasionally employed to better calculate particle surface area.
It is important to note that this calculation does not consider porosity. It is advisable to use tools capable of measuring specific sample properties for a deeper understanding of surface area and porosity.
The last display of sieve equivalency is normally employed for those who are utilizing manual sieve measurements and want to convert to an automated method.

Image Credit: Vision Analytical Inc.
Circularity, Smoothness, and Aspect Ratio Histograms
Shape measurements can be size-independent. In such cases, these fraction measures scale from zero to one.
The graph below is a histogram demonstrating smoothness distribution, which measures irregularity in a particle’s perimeter. In this case, the value of zero “0” depicts a very un-smooth particle, and the value of one “1” depicts a very smooth particle.
Practically, users can assume that smoother particle distributions generally lead to better flowability. For specific applications, such as metal powders in additive manufacturing, identifying non-smooth particles is critical to ensure the quality of the final product.
Other fractional shape measurements include circularity, opacity, and aspect ratio. All these parameters are reported on a linear scale, with each bin displaying the recorded quantity of particles within the specified range.

Image Credit: Vision Analytical Inc.
Aspect ratio is also presented on a linear scale. Shown below is the bounding rectangle aspect ratio. Particle shape analyzers typically offer several types of aspect ratio measurements, allowing users to select the one most suitable for their particle shapes.
Aspect ratio measurements generally range between 1.00 and 10, but these ranges can be user-defined. Similarly, the spacing of the bins in the histogram can also be adjusted by the user to suit specific analysis needs.

Image Credit: Vision Analytical Inc.
As discussed earlier, the reporting of number-weighted and volume-weighted distributions provides valuable insights into particle characteristics. Volume-weighted histograms emphasize larger particles due to their greater volume compared to the numerous smaller particles. This makes volume-weighted histograms particularly useful for identifying small amounts of agglomerates within a sample.
In contrast, number-weighted histograms highlight smaller particles, making them helpful for detecting large quantities of fines that could lead to issues like clogging or filtration problems. Using dynamic image analysis, objective evidence of these particles is provided through thumbnail images of every measured particle.
The following chart illustrates why a single sample can have distinct number-weighted and volume-weighted histograms. It also highlights the importance of analyzing both types of weighted statistics.
The combined use of number and volume weighting enables users to observe and understand small quantities of agglomerates (larger particles) and high quantities of fines (smaller particles), offering a comprehensive view of the sample.

Image Credit: Vision Analytical Inc.
More on Statistics
A typical statistical result not only gives the graphical histogram, but also will report a large amount of data. Below is a sample of a size-based histogram and associated data.

Image Credit: Vision Analytical Inc.
A typical size distribution is characterized by different values, one of the most common being the mean size. A mean value provides some information about particle size but does not indicate the shape of the distribution or how broad or narrow it is. The number or arithmetic mean is purely the average value and is frequently denoted as D1,0. Other means take into account volume weighting and area.
Assuming particle sphericity, the generic definition of a weighted Dp,q mean diameter is:

Definition of Dp,q means
The diameter means that are most often of use in characterizing a particle sample are:

In these descriptions, ni is the count in size bin number i, and di is the representative diameter of that size bin. The sums are over all particles, and N is the particle count total.
Definitions of these means in words are shown below:
Arithmetic mean diameter, D[1,0]: The average of all particle diameters in the sample.
Surface mean diameter, D[2,0]: The diameter of a particle whose surface area equals the sample’s total surface area if multiplied by the total number of droplets.
Volume mean diameter, D[3,0]: The diameter of a particle whose volume will equal the sample’s total volume if multiplied by the total number of particles.
Surface moment mean diameter, D[3,2] (“Sauter mean”): The diameter of a particle with the same volume-to-surface area ratio as the complete sample, calculated as D3,2 = 6 * (total volume/total area).
Volume moment mean diameter, D[4,3]: An indicator weighted on particle volume; the mean value most commonly used by laser diffraction tools.
Mode: The most common size in the simple.
Harmonic mean: Calculated as N / Σ (ni / di)
Geometric Means
Geometric means represent the visual weighting on a logarithmic size axis. The geometric mean diameter aligns with the center of a distribution on a log scale, whereas the arithmetic mean often appears lower on the size scale due to the higher prevalence of smaller particles compared to larger ones.

Image Credit: Vision Analytical Inc.
Employ the logs of the x-axis values (log [di] in place of di) to calculate the geometric mean:
The geometric mean = Σ [ni log(di)] / N
The geometric versions of the other means and standard deviation can be computed using the same technique.
Measures of Spread
Standard deviation determines distribution width:

Where μ = mean diameter (D10). It has units of μm for size distribution.
The coefficient of variation (CV) is the ratio of the standard deviation to the mean: CV = σ/μ. To express as a percent multiplied by 100. This statistic does not have units as it is a ratio.
Percentiles
Percentiles conduct size data as one or more numbers. The median size divides the particles into two portions comprising equal counts—the number median, also known as the 50th or the 50 % percentile.
The 10th percentile outlines the size with the property that 10 % of the particle count is less than that size. Percentiles can be defined in a similar way for any other value.
Commonly, the 10th, 50th, and 90th percentiles are used for characterization, providing a simple yet informative alternative to a single mean. Additional percentiles are available and can be customized in the Insight software to meet specific industry requirements.
The volume median—or 50th percentile by volume—divides the sample’s volume into two equal pieces. The two classes will have equal volume but not equal particles.
Other volume percentiles are characterized in a similar manner. The 25th volume percentile, for example, means that particles smaller than this size make up a quarter of the sample’s total volume.
Other Characterizations
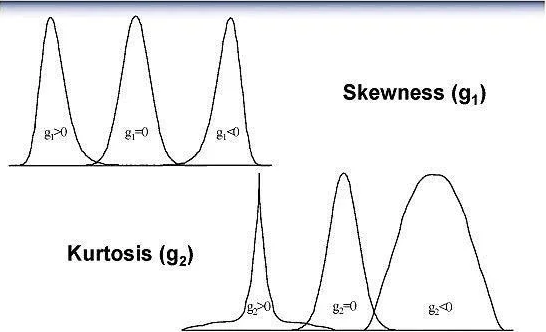
Image Credit: Vision Analytical Inc.
Skewness is an indicator of how asymmetrical the shape of the distribution is, about the center. A positive skewness value suggests a longer tail on the right side of the center, while a negative value indicates a tail on the left.
Skewness = Σ ni (di – μ)3 / (σ3 N) (σ = std. dev., μ = mean)
Kurtosis is an indicator of how much the shape differs from the typical bell curve in a vertical sense.
Kurtosis = [Σ ni (di – μ)4 / (σ4 N)] / – 3 (σ = std. dev., μ = mean)

This information has been sourced, reviewed and adapted from materials provided by Vision Analytical Inc.
For more information on this source, please visit Vision Analytical Inc.