Introduction Well-ordered latex particle films have been of significant technological interest for a long time [1-6]. How the solvent evaporation process affects the structure of the film is not well understood. The irreversible nature of the evaporation process necessitates the use of nonstandard theoretical methods and analysis of even simple models is nontrivial. In our previous work [6] a simple method to study the growth kinetics and structure of colloidal films has been presented. The main features of the model are mentioned here and its details can be found elsewhere [6]. A simulation box prism of side Lx=Ly=30d and length L=12d is filled with N=3000 identical colloids of unitary diameter, d=1, considered as hard spheres so, overlapping among them is not allowed, see Figure 1. 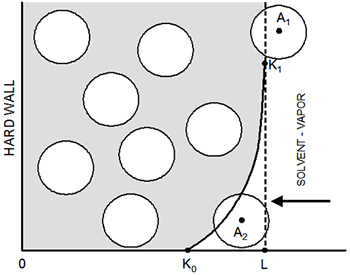
Figure 1. Schematic representation of the simulation box: curve K0-K1 indicates the region of the effective potential due to the vapor-liquid interface; particle A2 is in the zone of the soft potential, A1 is ‘frozen’ (immobilized) because its location in vapor phase. The interaction of the colloid particles with the liquid-vapor interface, Uic, (right-hand wall of Figure 1) was simulated as an effective external field, by using a soft repulsive potential:  (1) (1)
where z is the normal distance from the center of a polymer particle to the interface; n is a parameter of softness that can be related with the system temperature [6]. The parameter n was kept constant at n=8. Unlike the Ref. [6], here we consider an attractive wall surface: wall-colloid interaction is modeled through the attractive Yukawa interaction,  (2) (2)
where parameters K and A are related with the strength and the length of the potential, respectively; they have been chosen to be K =-5 and A=3. We have considered particle MC displacement to be qualitatively related to the viscosity of the continuous media: high maximum displacement, Δl, (and low acceptance of particle translation [7] at densities considered) corresponds to high viscosity. The rate of movement of the liquid-vapor interface is related to the rate of drying of the film. The MC step is considered as a time parameter. In other words, after each particle of the system is allowed to try to move ν times according to Metropolis algorithm [7], the interface moves reducing the film thickness by step Δi=0.01 and increasing the film density. This artifice emulates both water evaporation and subsequent increment of solid content during the film formation process. Results In Figure 2 the density profiles for two drying rates with the same particle displacement are presented. At rapid drying, ν=2, the density of colloidal particles in the interface is high during all the drying process, because most of the particles cannot escape from the influence of the interface. For ν=48 the final film density profile, at t=1150, shows that subsequent layers are clearly defined, which can be translated into a film with better protective properties. Furthermore, at ν=2 some particles ‘freeze’ before the process is terminated, reducing the final density of the colloidal layers. 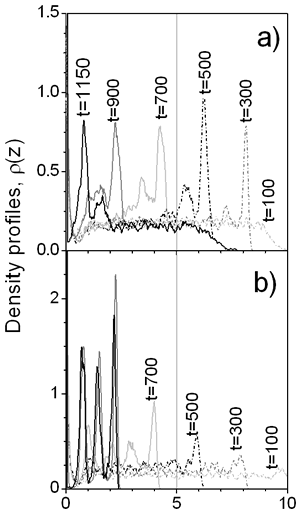
Figure 2. Density profiles for a) Δ=2 and b) ν=48 with Δ l=0.05. The evolution of the first layer density over the substrate is shown in the Figure 3 for slow and faster drying rates as well as for different viscosities (Δl). As can be seen at the high drying rate (ν=2) the viscosity of the continuous media has a great influence on the density of the layer: the lower the viscosity the higher is the density of the layer. If the displacement of the particles is small, due to high solvent viscosity, it is difficult for the first monolayer to gain particles, even at moderate vaporization rate, ν=8. But as the drying rate decreases, the influence of the solvent viscosity is reduced. This is because of the time that each particle has to rearrange before the vapor-liquid interface displaces. In the same picture, one can see that the first layer saturates before evaporation process is completed. 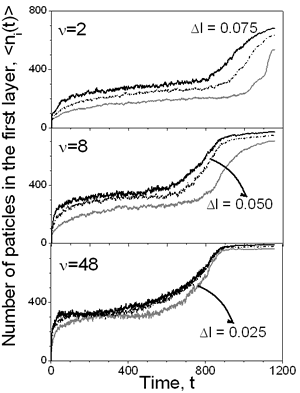
Figure 3. Evolution of the number of particles in the layer over the substrate as a function of time for different conditions, e.g. drying rate and maximum particle displacement. The influence of the vaporization rate and the viscosity on the final properties of the film can be deduced from Figure 4, too. If ν=2 the subsequent layers are poorly defined, even for the largest displacement considered. Once again, these graphs show that at high drying rates, the viscosity of the solvent plays an important role in the film forming process. As the diffusion of the colloidal particles increases with increasing dryings rates, the final density of the layers increases too. However, for a moderate rate, ν=8, it is possible to observe that the formation of the different layers is improved: higher density with well defined layers. But with decreasing the drying rate, ν=48, the density in each layers increases and each pick becomes narrower, so better structured film is formed. 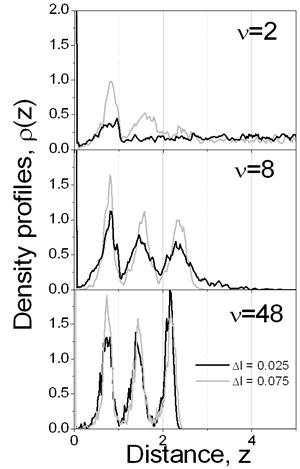
Figure 4. Final film density profiles, t=1150, at ν=2, 8 and 48. In the snapshots of Figure 5 typical configurations of the first layer over substrate is shown. It is clearly seen that a more organized structure is obtained at a slow drying rate, ν=60. Indeed, one can observe the (100) face of the fcc structure and some regions where the hexagonal arrangement is predominant. It is interesting to note that if slower drying rates are used, the cubic structure is preferred; such structure is manifested by the small pick appearing in the in-layer two-dimensional radial distribution function at r=√2. The recent experimental observations [1, 3-5] confirm such coexistence of hexagonal and tetragonal domains of dried latex films. Besides, it has been claimed [3, 5] that the solvent evaporation rate is one of the important factors influencing the crystallization process of latex particles. 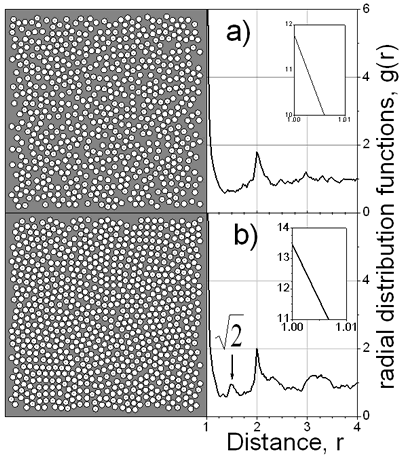
Figure 5. Snapshots at ν=48 and b) ν=60 with Δl=0.050. Conclusions Computer simulations of colloidal dispersions using a kinetic MC method were performed. The influence the drying rates and the diffusion of the colloidal particles on the structure of the final latex films was studied. The viscosity of the continuous media is found to be important at high drying rates. The impact of the viscosity is reduced as the drying rate is decreased. In order to obtain well-ordered layers with high density it is necessary to use slow drying rates. Although the model is highly simplified in comparison to the experimental situation, it is able to reproduce some trends of latex film formation. We believe that the sophistication of the interactions between particles may put the model somewhat closer to the experimental results. In this way as a next step, we plan to model the colloid-colloid interaction through the soft repulsive potential. References 1. M. A. Winnik, “The formation and properties of latex film” in Emulsion Polymerization and Emulsion Polymers, (Ed. P.A. Lovell and M.S. El-Aasser), John Wiley & Sons Ltd, UK, (1997) 467-515. 2. R. P. A. Dullens, E. M. Claesson and W. K. Kegel, “Preparation and Properties of Cross-Linked Fluorescent Poly(methyl methacrylate) Latex Colloids”, Langmuir, 20 (2004) 658-664. 3. C. D. Dushkin, G. S. Lazarov, S. N. Kotsev, H. Yoshimura and K. Nagayama, “Effect of Growth Conditions on the Structure of Two-dimensional Latex Crystals: Experiment”, Colloid. Polym. Sci., 277 (1999) 914-930. 4. P. Pieranski, L. Strzelecki and B. Pansu, “Thin Colloidal Crystals”, Phys. Rev. Lett., 50 (1983) 900-903. 5. A. H. Cardoso, C. A. Paula Leite, M .E. Darbello Zaniquelli and F. Galembeck, “Easy Polymer Latex Self-assembly and Colloidal Crystal Formation: the Case of Poly[styrene-co-(2-hydroxyethyl methacrylate)]”, Colloid and Surf., A 144 (1998) 207-217. 6. Y. Reyes and Y. Duda, “Modeling of Drying in Films of Colloidal Particles”, Langmuir (2005) in press. 7. D. P. Landau and K. Binder, “A Guide to Monte Carlo Simulations in Statistical Physics”, Cambridge University Press, UK, (2000) pp. 7-47. Contact Details |