In a recent article published in the open-access journal Coatings, scientists proposed a film formation model as well as a numerical simulation method based on the computational fluid dynamics (CFD) theory to predict the thickness of airless spraying robots. The film formation model was introduced to numerical simulation, and the properties of the coating film and the spray flow field were analyzed on the basis of the CFD method. The results of this method were verified as similar to that of a spray gun.
Study: Modeling and Characteristics of Airless Spray Film Formation. Image Credit: Pixel B/Shutterstock.com
Background
Airless spraying has several merits, including spraying surface quality, high paint utilization rates, construction efficiency, and strong adhesion. The airless spraying robot, however, faces problems such as undesirable spraying trajectory on complex surfaces, incorrect simulation of spray thickness, and inability to quality control the coating film.
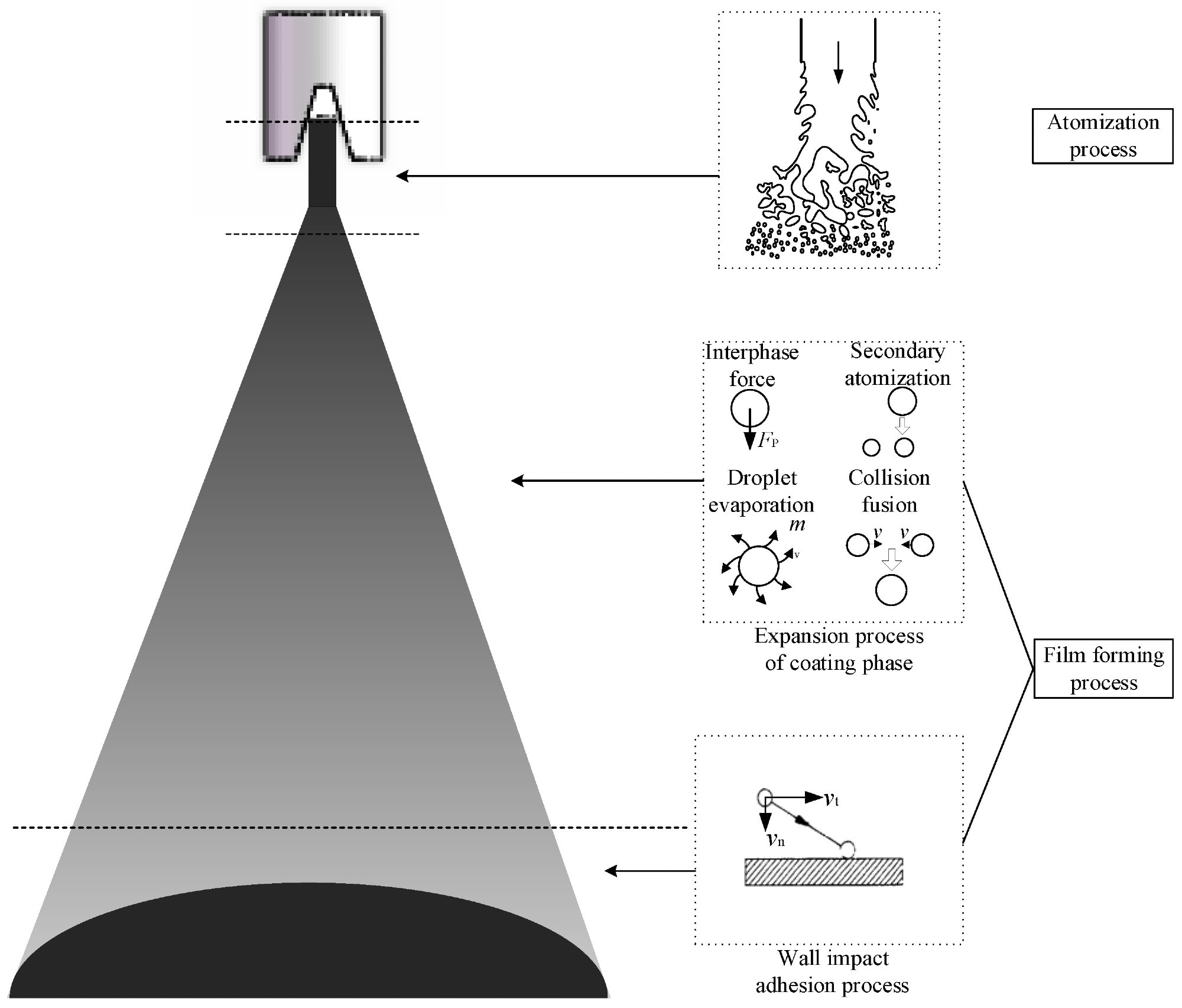
Airless spraying process. Image Credit: Yang, G et al., Coatings
The CFD method forms the basis of research on the model of film formation. The methodical approaches implemented in the treatment of paint droplets are the Eulerian-Lagrangian approach and the Eulerian-Eulerian approach. The Eulerian-Eulerian approach can inspect each phase’s turbulent motion process with detailed information on the droplet phase’s spatial distribution.
The present study explores a reasonable model for film formation and airless spraying characteristics that can be used for predicting the thickness of spraying robots based on the CFD method.
About the Study
In this study, researchers prepared the film formation model by incorporating the airless spraying process, the paint expansion model, the turbulence model, and the wall impact model. The airless spraying process constituted paint atomization, which was not the focus of the study, and paint film formation, which consists of the paint phase expansion and the formation of the impact film by paint droplets. The paint expansion modeling considered negligible mass and heat transfer, while the continuum surface stress (CSS) model was used to calculate the surface tension. Near-wall impact model was described using the standard wall function method, while the liquid film model was established using the Eulerian wall film (EWF) model.
Additionally, the numerical simulations were set in an environment of 1 atm, with the first phase set to the air phase and the second one set to the paint phase. The dynamic settings were unchanged from those of the plane spraying.
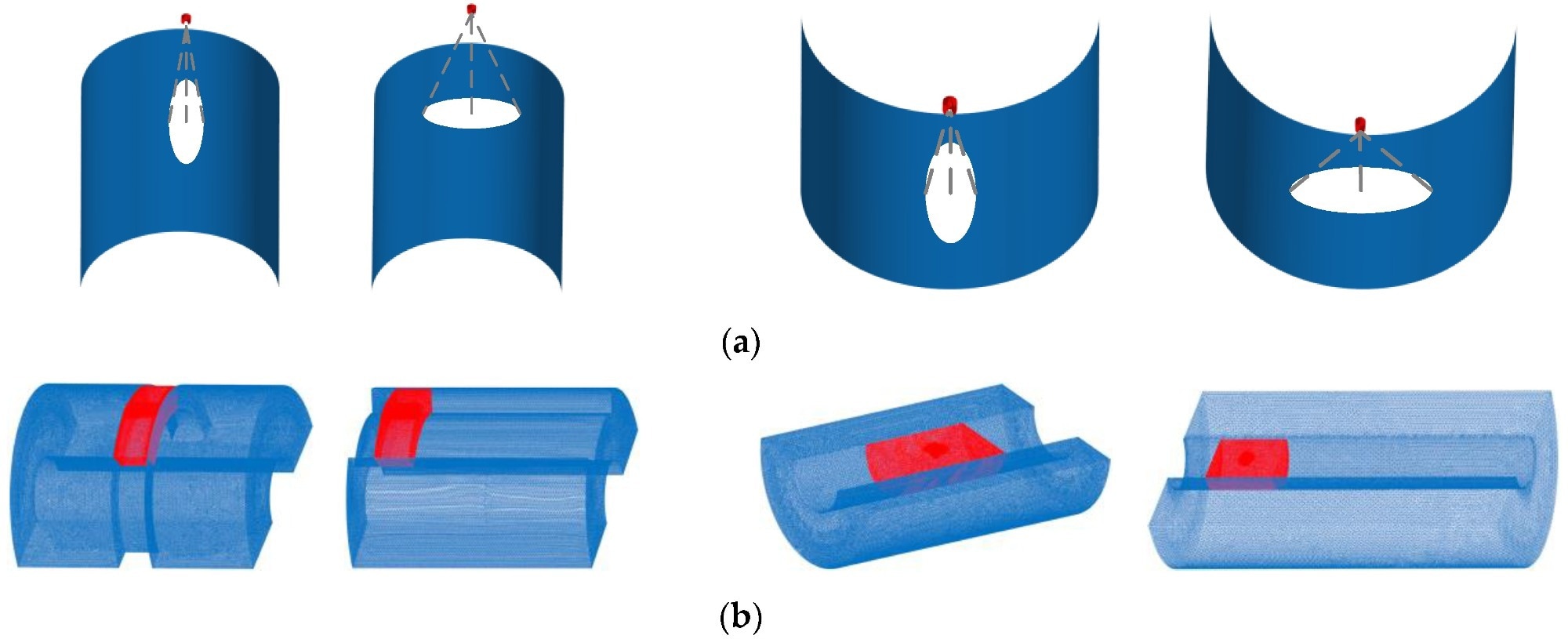
Computational domain and mesh division of the arc surface spraying. (a) Computational domain. (b) Meshing. Image Credit: Yang, G et al., Coatings
Observations
The spray flow was divided, based on the jet’s characteristics, into the free jet, impact, and wall flow regions. With no difference between the free jet and the paint, the team observed the paint hitting the wall vertically in the impact zone and becoming almost horizontal while entering the wall zone. Moreover, the velocity distribution contours showed a wider spray flow field on the long axis than on the short axis, while the pressure distribution was substantially greater than that of the outer surface.
The researchers also noted that the arc surface coating film differed from the flat coating film. The increase in the spraying distance decreased the impact zone’s film thickness. In the case of dynamic coating films, the thickness of the coating on the flat surface was greater than that of the flat surface. Increased spray speed decreased the film thickness as a result of slower paint deposition at each point.
The numerical simulation results were verified by carrying out dynamic and static experiments on arc and plane surfaces, respectively. The vertical distance between the workpiece and the spray gun was unchanged, while the spraying robot’s trajectory was in line with the simulation’s motion situation. The resultant coating film had high gloss, with no visible wrinkle, particle bulge, bubble, and needle eye on the surface of the film.
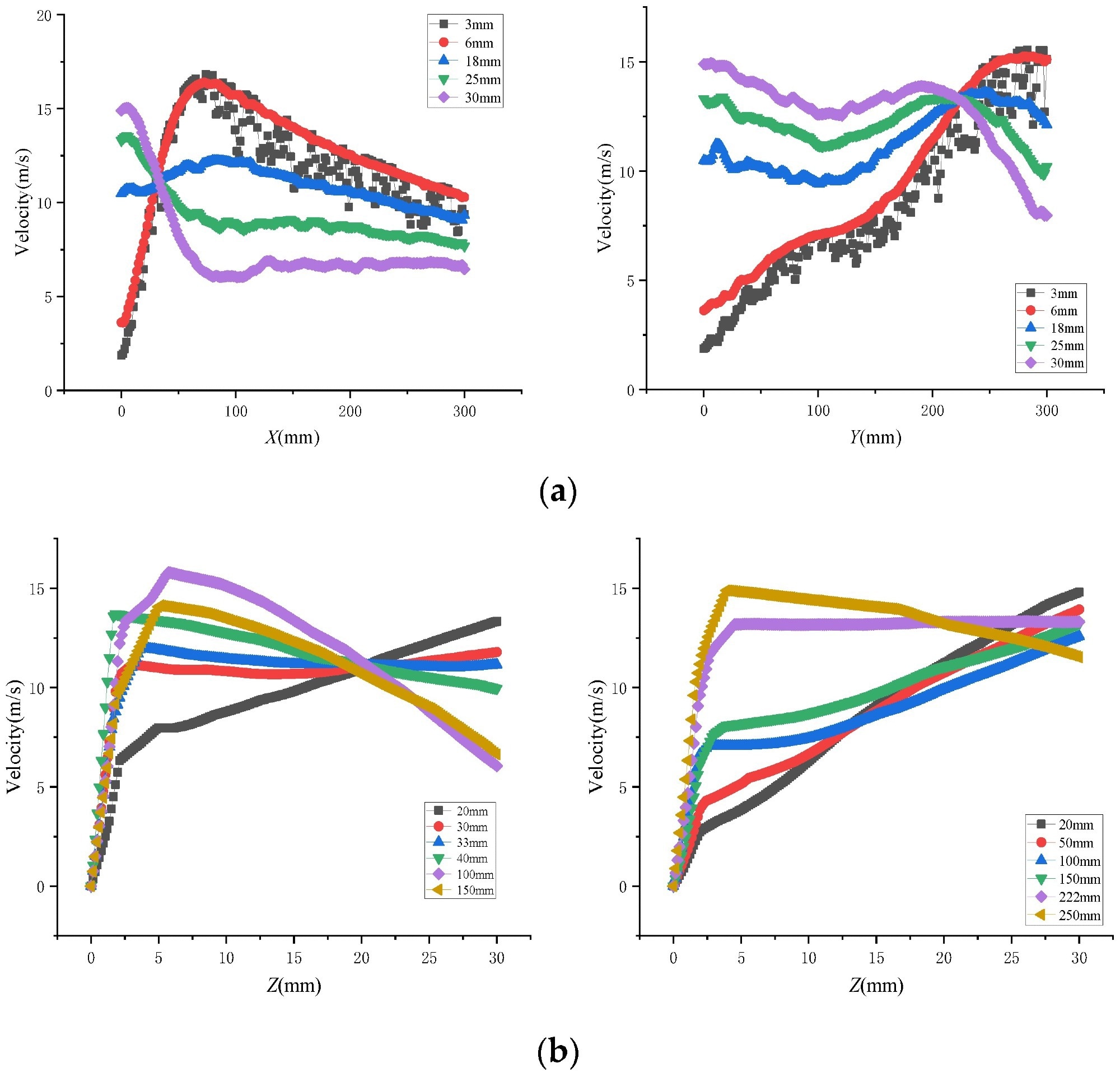
Velocity distributions. (a) Cross-sectional velocity. (b) Longitudinal-section velocity. Image Credit: Yang, G et al., Coatings
Conclusions
To sum it all up, similar pressure distributions were observed between the long-axis directions of circumferential spraying and the short-axis direction of the busbar spraying when sprayed on the outer surface. The inner surface spraying characteristics were contrary to the outer surface spraying. The greater the spraying pressure, the greater the coating area and the film thickness in static spraying. The increase in arc surface diameter increased the outer surface thickness and decreased the inner surface thickness in dynamic spraying.
According to the authors, the results of the numerical simulation were in line with that of the experiment, which established the accuracy of the film formation model of airless spraying, including the wall impact and the paint expansion models.
Source
Yang, G.; Wu, Z.; Chen, Y.; Chen, S.; Jiang, J. Modeling and Characteristics of Airless Spray Film Formation. Coatings 2022, 12, 949. https://doi.org/10.3390/coatings12070949
Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.