Scientists Discuss Cubene Crystals and their Properties

By Chinmay ChariReviewed by Susha Cheriyedath, M.Sc.Jul 18 2022

In a paper recently published in the open-access journal Materials, researchers described two cubene fullerite crystals, one belonging to the triclinic system and the other belonging to the cubic system, based on relaxational molecular dynamics. They also determined the mechanical properties of a cubene crystal.

Study: Mechanical Properties of Cubene Crystals. Image Credit: Leonid Andronov/Shutterstock.com

Background

Carbon molecules such as the C₆₀ and C₇₀ molecules are part of the fullerene family. Although it is easier to obtain fullerenes with a larger number of carbon atoms, with C₂₀ being the smallest spherical fullerene, a cube-shaped C₈ molecule termed cubene is likely the smallest fullerene. A fullerene-based molecular crystal is called a fullerite.

Fewer studies have been conducted on cubenes and cubanes C₈H₈ than the rest of the fullerenes. With a bond angle of 90° being energetically unfavorable, the cubene molecule is under high strain but should be stable as its energy relates to a deep minimum.

Fullerites possess multiple potential mechanical, chemical, and physical characteristics for various applications. High temperature and pressure polymerization of fullerites produce severely hard materials with bulk moduli ranging from 454 GPa to 644 GPa. The structure of fullerite crystals determines their properties, thus necessitating their research. Several studies have been conducted to analyze and predict the structure of C₆₀, C₇₀, and C₈H₈ fullerites, but there has been no information on the structure of C₈. This study presents the mechanical and physical properties of C₈, which could be potentially used for applications such as hydrogen storage.

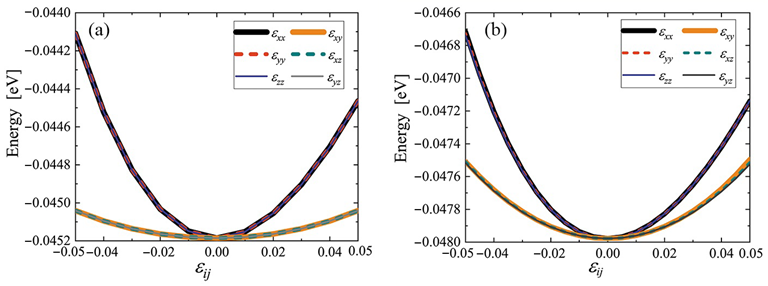
Potential energy per atom of cubic (a) and triclinic (b) cubene crystals depending on strain ε_ij. Only one component of the strain tensor is varied, the rest are equal to zero. Image Credit: Galiakhmetova, L.K et al., Materials

Materials and Methods

In the present study, researchers simulated the cubene crystals’ mechanical properties and structure using molecular dynamics. The harmonic potential described the carbon-carbon interactions whereas the Lennard-Jones potential described the non-valence interactions.

Perturbative relaxational molecular dynamics were used to determine the equilibrium phases of the cubene crystal. Initially, randomly oriented cubenes are set in the face-centered cubic (fcc) lattice following periodic boundary conditions. The atom positions are perturbed, distancing the system from a local potential minimum, followed by relaxation of the structure to a deeper energy minimum.

The interatomic potentials in cubenes were defined by van der Waals bonds which are weaker than covalent bonds by two orders of magnitude, due to which harmonic potential was deemed sufficient to analyze the covalent bonds. The stress components, elastic constants, and potential energy of the crystals were calculated as the functions of homogeneous deformation. To sum it up, the research found the equilibrium phases followed by the analysis of their stability in relation to uniform deformation, and subsequently, the phase properties such as stress-strain curves, elastic constants, and potential energy were computed.

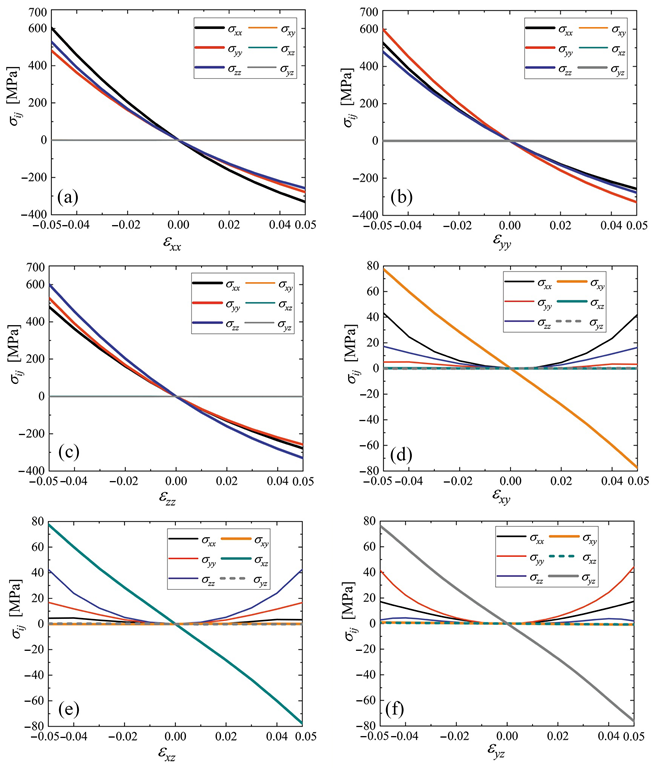
Stress–strain curves for cubic cubene crystal. Only one component of the strain tensor is varied, and the rest are equal to zero. The normal stress components are shown by black (σ_xx), red (σ_yy), and blue (σ_zz) lines. The shear stresses are plotted by yellow (σ_xy), cyan (σ_xz), and gray (σ_yz) lines. In some cases, dashed lines are used to show overlapping curves. Panels (a–f) correspond to changing ε_xx to ε_yz, respectively. Image Credit: Galiakhmetova, L.K et al., Materials

Observations

The team observed that the structural relaxation resulted in metastable structures having relatively greater potential energy in numerous cases. Some cases resulted in two equilibrium phases that had relatively low potential energies, with one of them belonging to the triclinic system, and the other to the cubic system.

Additionally, the potential energy per atom of the triclinic phase was 0.0028 eV lower than that of the cubic phase but was also lower among the randomly oriented structures obtained by relaxation. However, both the triclinic and cubic crystals were structurally stable at up to +/-5% strain.

Examining the elastic constants determined the triclinic crystal to be weakly anisotropic while being stiffer than the cubic crystal owing to its higher density. Furthermore, under normal strain, the shear stresses equaled zero in the cubic crystal as opposed to that in the triclinic crystal. An almost linear dependence of the elastic constants on the normal strain components was observed, while that on the shear strain components was weaker. The thermal vibration stability of the structures was not evaluated in this work.

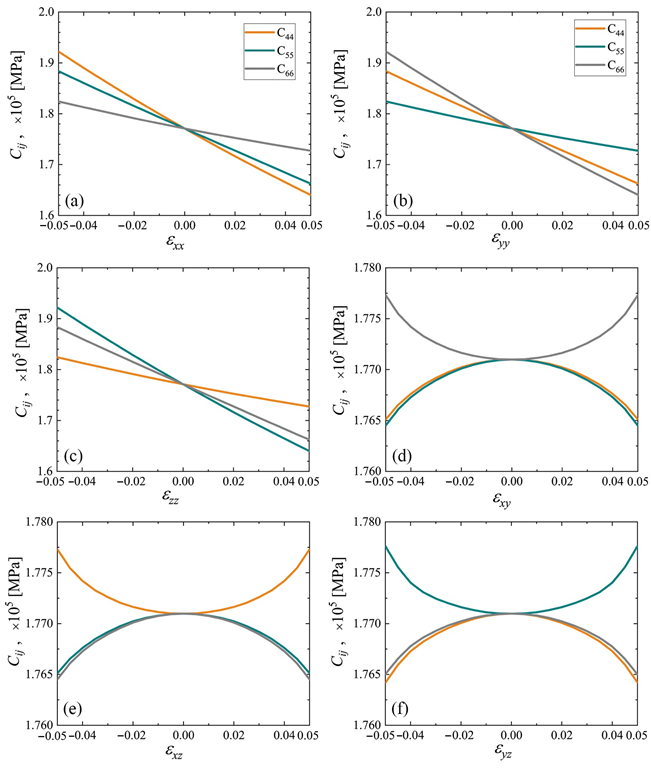
Elastic constants C₄₄, C₅₅, and C₆₆ as the functions of strain for cubic cubene crystal (yellow, cyan, and gray lines, respectively). Only one component of the strain tensor is varied, the rest are equal to zero. Panels (a–f) correspond to changing ε_xx to ε_yz, respectively. Image Credit: Galiakhmetova, L.K et al., Materials

Conclusions

To summarize, two equilibrium phases of the C₈ fullerite crystal, one belonging to the cubic system and the other to the triclinic system, were discovered. Under a +/-5% uniform strain, both phases were found to be stable. The energy per atom for the cubic phase was higher than that of the triclinic phase. While the cubic crystal was established to be metastable, the triclinic crystal was presumed to be in the crystalline phase.

However, this study had a few limitations due to the use of harmonic potential, which prevented the modeling of the structural transformation due to polymerization. The temperature influence was also unaccounted for, as a result of which the structures’ thermal stability range could not be ascertained.

According to the authors, the results of this study will stimulate further research on the physical characteristics of cubenes, including temperature effects, thermal expansion, and vibration spectra.

Disclaimer: The views expressed here are those of the author expressed in their private capacity and do not necessarily represent the views of AZoM.com Limited T/A AZoNetwork the owner and operator of this website. This disclaimer forms part of the Terms and conditions of use of this website.