A new study under the direction of Professor Barak Kol of the Hebrew University's Racah Institute of Physics establishes a novel method for comprehending the dynamics of non-hierarchical three-body systems.
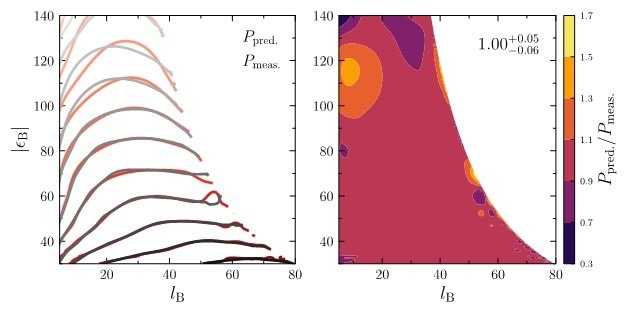Validation figure. Left: contours of predicted and measured chaotic outcome distribution in a bi-variate space describing the motion of the outgoing binary. Right: the ratio of the predicted and measured distributions. Both figures demonstrate strong validation. Image Credit: Barak Kol
The recently proposed flux-based statistical theory showed impressive predictive power for chaotic behavior, opening new avenues for more efficient calculations and an in-depth understanding of intricate systems.
The study sought to validate a hypothesis about the behavior of three-body systems, putting forward that chaotic results in these systems may be anticipated by a formula utilizing a known function called the asymptotic flux and a chaotic emissivity function.
Researchers tracked millions of scattering events in simulations to determine the chaotic emissivity function and differentiate between chaotic and regular scattering. This procedure produced a trivariate absorptivity function, which served as a foundation for evaluating the chaotic outcomes predicted by the theory.
In addition to demonstrating a more effective, Kol considered an economized approach for estimating chaotic outcome distributions in complex systems; the findings closely matched the actual distribution, confirming the validity of the theory.
Three-body systems' chaotic nature has historically presented physicists with significant analytical and predictive difficulty. However, the new method provided by the flux-based statistical theory makes this complex issue easier to understand.
The central tenet of this theory is that the chaotic outcome distribution may be written as the known function of asymptotic flux multiplied by the chaotic emissivity function. This novel idea provides a path for more effective calculations and a more comprehensive comprehension of chaotic dynamics.
Millions of scattering events were carefully measured to determine the chaotic emissivity function, also known as absorptivity, by the research team using sophisticated simulations to verify the idea. They derived a trivariate absorptivity function by concentrating on events until the difference between regular and chaotic scattering could be identified.
The team successfully computed the flux-based forecast for the chaotic outcome distribution over binary binding energy and rotational momentum using these newly obtained data. Remarkably, the outcomes demonstrated a high degree of agreement with the measured distribution, offering thorough validation of the precision and potency of the flux-based hypothesis.
The three-body problem represents one of the oldest and most formidable puzzles in the realm of physics. In 2021, I authored an article presenting a novel theory aimed at providing a statistical solution. This approach challenged the foundational assumptions of preceding theories, introducing the concept of flux in the phase space and earning the title of the flux-based statistical theory. In this collaborative endeavor, we rigorously scrutinize and question the flux-based statistical theory through an extensive series of computer simulations.
Barak Kol, Professor, Racah Institute of Physics, Hebrew University of Jerusalem
Barak Kol explained, “The validation process showcases an impressive 6% accuracy across the entire two-dimensional space of variables examined. This exhaustive research establishes that the flux-based theory stands as the most precise statistical framework available for deciphering this intricate system. Indeed, it marks a significant stride forward in attaining precision and dependability in our comprehension of the three-body problem.”
This discovery has important ramifications for many other domains and represents a major turning point in the study of chaos theory. Here are a few instances:
- Celestial Mechanics: Comprehending these dynamics can significantly improve the capacity to statistically forecast and precisely model celestial motions.
- Astrophysics: It can contribute to the comprehension of astrophysical phenomena, including interactions between celestial bodies, the evolution of planetary systems, and the generation of gravitational waves.
The latest piece represents the conclusion of a series of five articles. Among them, a prior paper introduced new variables to simplify the problem formulation. An equivalent three-dimensional space in the form of a joint of three pipes takes the place of the nine variables in these variables that specify the locations of three bodies.
It is called geometry space because it describes the geometry of the triangle that the three bodies define. The rotating motion of the immediate place defined by the three bodies should be added to it. A magnetic-like force that depicts the Coriolis force and an electric-like force that describes the Newtonian gravitational forces are used to formulate motion in geometric space.
In conclusion, the fundamental understanding acquired from these investigations might have broad ramifications in disciplines dealing with complex dynamic systems, such as materials science and astronomy, among others.
Journal Reference:
Viraj Manwadkar, et.al., (2024). Measurement of three-body chaotic absorptivity predicts chaotic outcome distribution. Celestial Mechanics and Dynamical Astronomy. doi.org/10.1007/s10569-023-10174-z.